AB: Regelmäßige n-Ecke und n,k-Sterne (2)
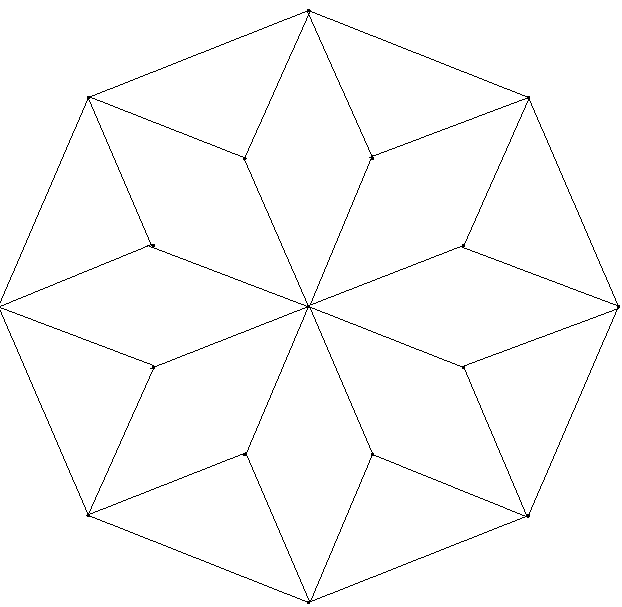
Achtecke: Gegeben sind 8 kongruente Rauten mit dem spitzen Winkel der Größe 45° und der Seitenlänge a sowie 8 gleichschenklig-rechtwinklige Dreiecke mit der Schenkellänge a. Parkettieren Sie unter Verwendung aller Teile damit:
ein regelmäßiges Achteck. Bestimmen Sie zunächst die Seitenlänge des Achtecks in Abhängigkeit von a. Wo tritt diese Länge bei den Einzelteilen auf?
Jede Raute hat den Flächeninhalt \(\frac{ { {a^2} } }{ {\sqrt{2} } }\), jedes Dreieck hat den Flächeninhalt \(\frac{ { {a^2} } }{2}\). 8 Rauten und 8 Dreiecke haben zusammen den Flächeninhalt 4a²⋅(1+√2). Ein Achteck mit er Seitenlänge b hat den Flächeninhalt 2b²⋅(1+√2). Dann ist b=a⋅√2. Das ist genau die Basis jedes der 8 Dreiecke. Diese werden an den Rand des Achtecks gelegt:
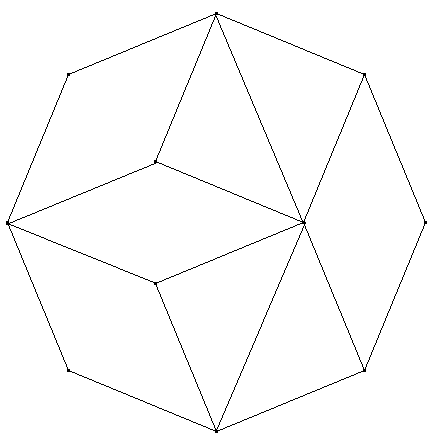
zwei kongruente regelmäßige Achtecke. Bestimmen Sie zunächst die Seitenlänge jedes der beiden Achtecke in Abhängigkeit von a. Wo tritt diese Länge bei den Einzelteilen auf?
Kongruente n-Ecke sind flächengleich. Jedes jetzt auszulegende Achteck hat den halben Flächeninhalt des Achtecks unter a). Die neuen Achtecke sind mit dem Faktor \(\frac{1}{ {\sqrt{2} } }\) zentrisch gestreckte Bilder des Achtecks unter a). Beide neuen Achtecke haben die Seitenlänge a und die nebenstehende Aufteilung.
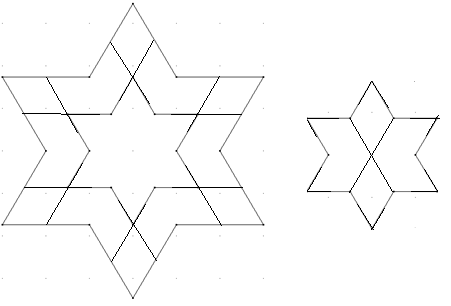
Die 6,2-Sterne: Die zwölf Seitenlängen des inneren Sterns sind genau halb so lang wie die zwölf Seitenlängen des äußeren Sterns. Zerlegen Sie den Streifen zwischen innerem und äußerem Stern mit 12 Schnitten so, dass aus den Teilen drei Sterne von der Form und der Größe des inneren Sterns zusammengesetzt werden können.

Bei dieser Aufteilung können aus den Einzelteilen drei weitere kleinere Sterne gelegt werden:
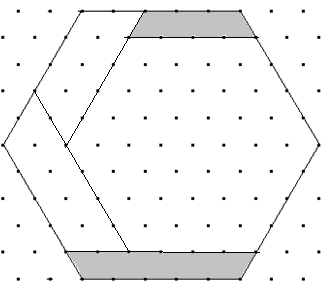
Sechsecke: Gegeben sind drei regelmäßige Sechsecke. Das kleinste Sechseck unten wird – wie dargestellt – in vier Teile zerlegt. Mit diesen vier Teilen und dem mittelgroßen Sechseck (links) lässt sich das rechte Sechseck (rechts) vollständig auslegen.
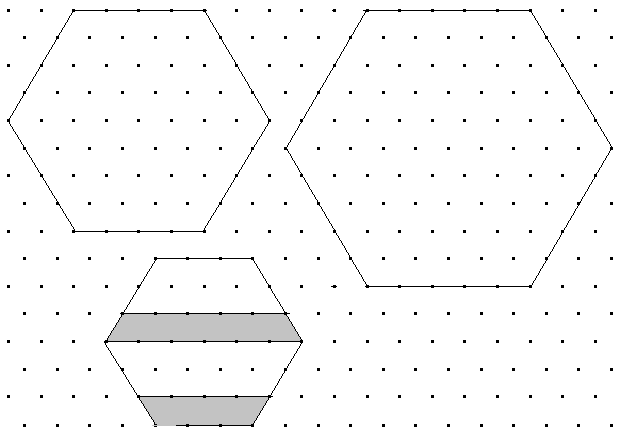
Führen Sie das Auslegen durch.
Welche notwendige Bedingung müssen die Seitenlängen der drei Sechsecke erfüllen, damit eine derartige Aufgabe lösbar ist?
Wenn a und b die beiden kürzeren Seitenlängen sind und c die längere, dann muss a²+b²=c² gelten.
Pentagramme: Zerschneiden Sie die vier kleinen Pentagramme in die dargestellten Teile und legen Sie das große Pentagramm mit den Teilen aus.

Das ausgelegte Pentagramm:

