AB: Lektion Grenzwerte (Teil 3)
Nachfolgend findet ihr Aufgaben zu Grenzwerten, mit denen ihr euer neues Wissen testen könnt.
Bestimme die Grenzwerte (schwer).
\( \lim\limits_{x\to\infty} \frac{7(x^2-2)^2}{x^4-2x} = \) \( 7 \)
Wenn man die binomische Formel erkennt, so erhält man im Zähler die höchste Potenz mit x4. Damit ist Zählergrad = Nennergrad und der Grenzwert 7.
\( \lim\limits_{x\to 12} \frac{12(x^2-144)}{x-12} = \) \( 288 \)
Hier haben wir die dritte binomische Formel vorliegen (im Zähler) und können schreiben x² - 144 = (x + 12)·(x-12). Damit kürzt sich der letzte Faktor mit dem Nenner und wir haben übrig:
\( \lim\limits_{x \to 12} 12·(x+12) \)
Nun liegt für x = 12 keine Problemstelle mehr vor und man kann einsetzen.
\( \lim\limits_{x\to0} \frac{7x(x^2-2)^2}{x^4-2x} = \) \( -14 \)
Hier wurde erst mit x gekürzt und dann x = 0 eingesetzt, da x = 0 keine Problemstelle mehr ist.
Existiert ein beidseitiger Grenzwert (graphische Argumentation)? $$ \lim\limits_{x\to7^{+}} \frac{3x^3-2x+4x^5}{x^2-14x+49} = \lim\limits_{x\to7^{-}} \frac{3x^3-2x+4x^5}{x^2-14x+49} $$
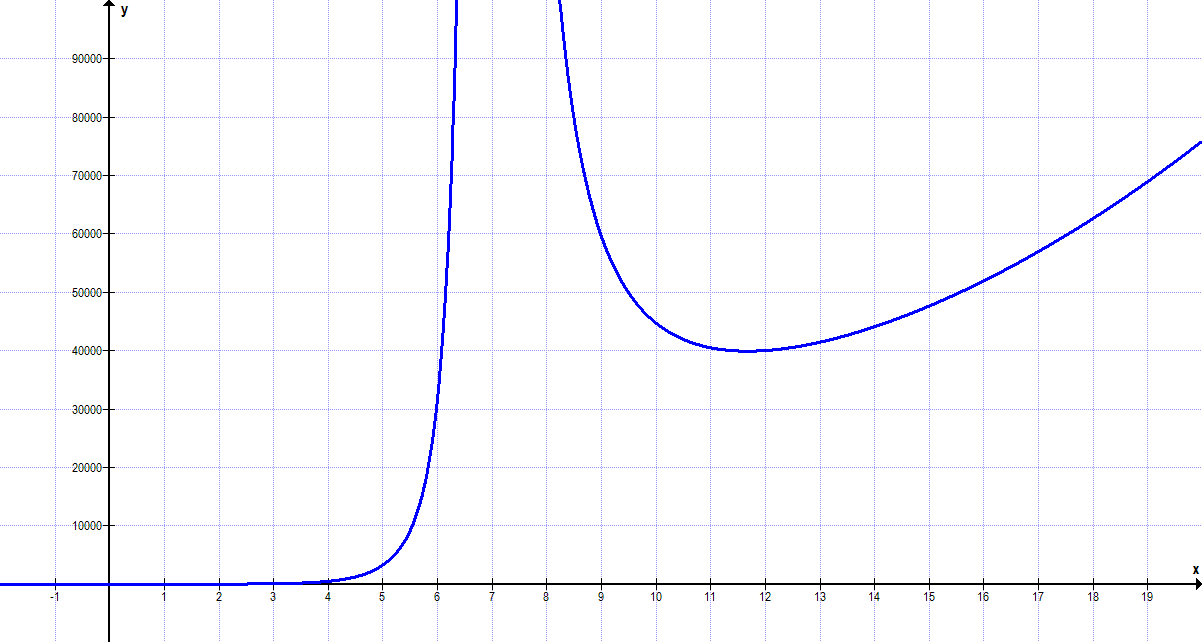
Da der Grenzwert auf beiden Seiten gegen +∞ geht, kann der Grenzwert angegeben werden als:
\( \lim\limits_{x\to7^{+}} \frac{3x^3-2x+4x^5}{x^2-14x+49} = \lim\limits_{x\to7^{-}} \frac{3x^3-2x+4x^5}{x^2-14x+49} = \lim\limits_{\textcolor{blue}{x \to 7}} \frac{3x^3-2x+4x^5}{x^2-14x+49} = ∞ \)
Existiert ein beidseitiger Grenzwert (graphische Argumentation)? $$ \lim\limits_{x\to4^{+}} \frac{1}{x-4} = \lim\limits_{x\to4^{-}} \frac{1}{x-4} $$
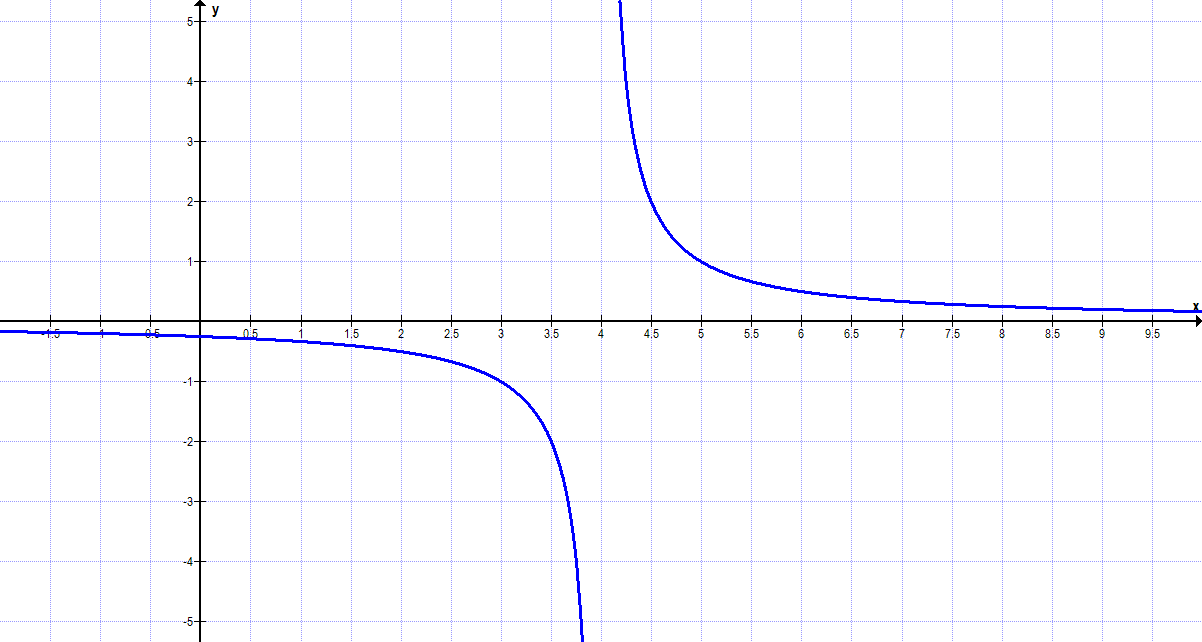
Es liegt kein beidseitiger Grenzwert vor.
