CHECK: Additionstheoreme II

Berechne den Wert von sin(135°) mit Hilfe eines passenden Additionstheorems.

$ \frac {\sqrt{2} } {3} $

$ \frac {\sqrt{2} } {2} $

$ -\frac {\sqrt{2} } {2} $

$ \frac {\sqrt{3} } {2} $

Wir zerlegen den Winkel von 135° in 90° und 45° und wenden das Additionstheorem für sin(α +β) an.

$$ sin(α +β) = sin(45° +90°) \\ = sin(45°) · cos(90°) + cos(45°) · sin(90°) \\ = \frac{ \sqrt{2} }{2} · 0 + \frac{ \sqrt{2} }{2} · 1 \\ = \frac{ \sqrt{2} } {2} $$

Für welche trigonometrische Funktionen kann man Additionstheoreme anwenden?

Nur für die Sinusfunktion

Nur für die Kosinusfunktion

Für alle trigonometrische Funktionen

Nur für die Tangens- und Kotangensfunktion

Additionstheoreme können für alle trigonometrischen Funktionen angewendet werden.

Welche Form des Termes in Abhängigkeit von tan(α) und tan(β) erhält man für tan(α+β), wenn man hierfür ein passendes Additionstheorem anwendet?

Eine Wurzel

Einen Bruch

Einen Summenterm

Einen Bruch:

$$ tan(α+β) = \frac {tan(α)+tan(β)} {1 - tan(α) · tan(β)} $$

Leite aus der Beschreibung bzw. Skizze das Additionstheorem für Sinus her.

Gegeben sind drei rechtwinklige Dreiecke ΔSCD, ΔSCA und ΔSAB mit den jeweiligen Innenwinkeln α, β und (α + β):

sin(α+β) = sin(α) + sin(β)

sin(α+β) = sin(α) · cos(α) + sin(β) · cos(β)

sin(α+β) = sin(α) · cos(β) + sin(β) · cos(α)

sin(α+β) = sin(α) · cos(β) - sin(β) · cos(α)

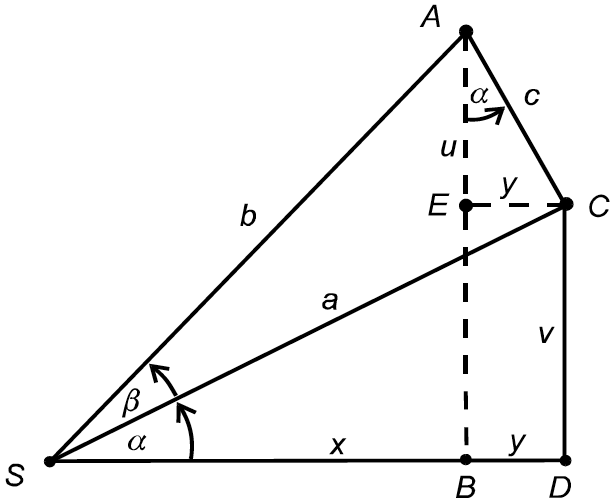
Gemäß Skizze ist |CD| = |EB|

$$ \sin(α+β) = \frac {|AB|} {|AS|} = \frac {|AE|+|EB|} {|AS|} = \frac {|AE|+|CD|} {|AS|} $$

$$ ⇒ \frac {|AE|} {|AS|} + \frac {|CD|} {|AS|} ⇔ \frac{|AE| · |AC|} {|AC| · |AS|} + \frac{|CD| · |CS|} {|CS| · |AS|} $$

Aus den Definitionen von Sinus und Kosinus folgt:

$$ \frac {|AC|} {|AS|} = \sin(β), \frac {|CD|} {|CS|} = \sin(α) \text{ und } \frac {|CC|} {|AS|} = \cos(β) $$

$$ \text{Winkel } EAC = α $$

$$ ⇒ \text{Winkel } SCB = \text{Winkel } ECA = 90° - α \\ ⇒ \text{Winkel } SCE = \text{Winkel } EAC= α $$

Daraus folgt

$$ \frac {|AE|} {|AC|} = \cos(α) $$

⇒ sin(α+β) = cos(α) · sin(β) + sin(α) · cos(β)

Berechne den Wert von tan(210°) über ein passendes Additionstheorem.

1

$ \sqrt{2} $

$ \sqrt{3} $

$ \frac{ \sqrt{3} }{3} $

tan(210°) = tan(180° + 30°)

Additionstheorem für Tangens:

$$ \tan(α+β) = \frac{ \tan(α) + \tan(β) } {1 - \tan(α) · \tan(β)} $$

$$ \tan(180° + 30°) = \frac{ \tan(180°) + \tan(30°)} {1 - \tan(180°) · \tan(30°)} $$

$$ \tan(180° + 30°) = \frac{0 + \tan(30°)}{1 - 0·\tan(30°)} = \frac{tan(30°)}{1} = \frac{ \sqrt{3} }{3} $$