CHECK: Einheitskreis III (schwierig)
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Wie sind die Terme sin(α) und cos(α) im Einheitskreis miteinander verknüpft?
(Hinweis: 0° ≤ α ≤ 360°)
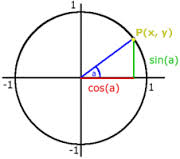
Laut Satz des Pythagoras gilt im dargestellten rechtwinkligen Dreieck, in dem der Radius r = 1 LE die Hypotenuse ist: sin²(α) + cos²(α) = 1
Bestimme die Koordinaten des Punktes P auf einem Einheitskreis unter einem Winkel α = 120°.
Die positive x-Achse schließt mit der Halbgeraden vom Ursprung zum Punkt P den Winkel α ein.
Koordinate x = cos(120°) = \( -\frac{1}{2} \)
Koordinate y = sin(120°) = \( \frac{1}{2} · \sqrt{3} \)
Auf dem Umfang eines Einheitskreises liegt ein Punkt P((\( \frac{1}{2}·\sqrt{2}\)) | (\( \frac{1}{2}·\sqrt{2} \))). Berechne den Winkel α.
Nutze die Winkelbeziehungen in einem rechtwinkligen Dreieck.
Gemäß den Winkelbeziehungen in einem rechtwinkligen Dreieck gilt hier:
sin(α) = y·Radius und cos(α) = x·Radius
Da im Einheitskreis der Radius 1 LE hat, gilt:
sin(α) = y und cos(α) = x
Mit:
$$ x = y = \frac { 1 }{ 2 } \sqrt { 2 } $$
folgt:
$$ sin(α) = cos(α) = \frac { 1 }{ 2 } \sqrt { 2 } $$
$$ α = arcsin( \frac { 1 }{ 2 } \sqrt { 2 })$$
α = 45°
Wenn wir \( \cos(α) = \frac { 1 }{ 2 } \sqrt { 2 } \) auswerten, bekommen wir ebenfalls den Winkel von 45° heraus.
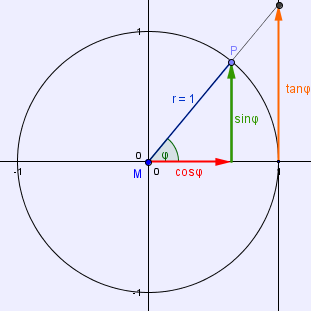
Es liegt ein Punkt auf dem Einheitskreis im I. Quadranten. Wo wird hier der Tangens abgelesen?
Siehe Skizze:
Fortschritt:
