CHECK: Gebrochenrationale Funktionen
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Wann hat eine gebrochenrationale Funktion ganz sicher eine Definitionslücke?
Zähler ungleich 0 und Nenner gleich 0.
Gesucht ist die Nullstelle der Funktion \( f(x) = \frac{2x - 2} {x + 2} \)
(2x-2)/(x+2) = 0 | ·(x+2)
(2x-2) = 0
2x - 2 = 0 | +2
2x = 2 | :2
x = 1
Vergleiche auch Graph der Funktion:
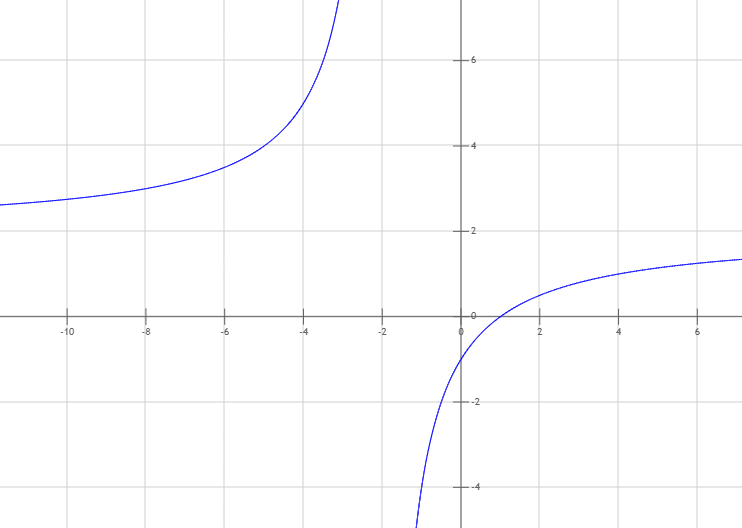
Bestimme die Nullstelle der gebrochenrationalen Funktion \( f(x) = \frac{2-3x}{1+x} \)
Für eine exisierende Nullstelle muss der Zähler der gebrochenen Funktion den Wert Null annehmen:
$$ f(x) = \frac{g(x)}{h(x)} = 0 \Longleftrightarrow g(x) = 0 \text{ und } h(x) ≠ 0 $$
$$ g(x) = 2 - 3x = 0 \Longrightarrow x = \frac{2}{3} $$
Das ist die gesuchte Nullstelle.
Fortschritt:
