CHECK: Quadratische Gleichungen IV
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
In welcher Höhe befindet sich die Knickstelle?
Ein 10 m hoher Mast wurde vom Sturm durchgebrochen bzw. geknickt, wobei die Höhe der Knickstelle ermittelt werden soll. Die Spitze des Mastes berührt den Erdboden 5 m vom Fußpunkt des Mastes entfernt. In welcher Höhe befindet sich die Knickstelle?
Zeichnen wir zuerst eine Skizze und stellen dann die Gleichung auf:
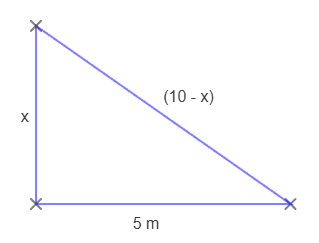
Aufstellen vom Satz des Pythagoras:
x2 + 52 = (10 - x)2
Diese gelöst:
x2 + 25 = (10 - x)2
x2 + 25 = 102 - 2·10·x + x2
x2 + 25 = 100 - 20·x + x2 | -x2
25 = 100 - 20·x | -100
-75 = -20·x
-20·x = -75 | : (-20)
x = 3,75
Löse die quadratische Gleichung: 2x² - 8x + 10 = 4
2·x² + (-8)·x + 6 = 0 | :2
2·x²:2 + (-8)·x:2 + 6:2 = 0
1·x² + (-4)·x + 3 = 0
p = -4 und q = 3
Lösung mit p-q-Formel:
x1,2 = -(p⁄2) ± √((p⁄2)² - q)
x1,2 = -(-4⁄2) ± √((-4⁄2)² - 3)
x1,2 = 2 ± √1
Lösungen:
x1 = 2 + 1 = 3
x2 = 2 - 1 = 1
Löse die quadratische Gleichung: 1,8·x² + (-7,4)·x + 4,8 = 4
1,8·x² + (-7,4)·x + 0,8 = 0 | :1,8
1,8·x²:1,8 + (-7,4)·x:1,8 + 0,8:1,8 = 0
1·x² + (-4,11111)·x + 0,44444 = 0
p = -4,11111 und q = 0,44444
Lösung mit p-q-Formel:
x1,2 = -(p⁄2) ± √((p⁄2)² - q)
x1,2 = -(-4,11111⁄2) ± √((-4,11111⁄2)² - 0,44444)
x1,2 = 2,05555 ± √3,78087
Lösungen:
x1 = 2,05555 + 1,94445 = 4
x2 = 2,05555 - 1,94445 = 0,1111
Bestimme die Lösung der quadratischen Gleichung: 3·x² + -2·x + -7 = 1
Berechnung der Normalform:
3·x² + (-2)·x + (-8) = 0 | :3
3·x²:3 + (-2)·x:3 + (-8):3 = 0
1·x² + (-0,66667)·x + (-2,66667) = 0
p = -0,66667 und q = -2,66667
Lösung mit p-q-Formel:
x1,2 = -(p⁄2) ± √((p⁄2)² - q)
x1,2 = -(-0,66667⁄2) ± √((-0,66667⁄2)² - (-2,66667))
x1,2 = 0,33333 ± √2,77778
Lösungen:
x1 = 0,33333 + 1,66667 = 2
x2 = 0,33333 - 1,66667 = -1,33334
Bestimme die Lösung der quadratischen Gleichung: -x² + 3·x + 4 = 0
Berechnung der Normalform:
(-1)·x² + 3·x + 4 = 0 | :(-1)
(-1)·x²:(-1) + 3·x:(-1) + 4:(-1) = 0
1·x² + (-3)·x + (-4) = 0
p = -3 und q = -4
Lösung mit p-q-Formel:
x1,2 = -(p⁄2)
± √((p⁄2)² - q)
x1,2 = -(-3⁄2)
± √((-3⁄2)² - (-4))
x1,2 = 1,5 ± √6,25
Lösungen:
x1 = 1,5 + 2,5 = 4
x2 = 1,5 - 2,5 = -1
Fortschritt:
