CHECK: Symmetrie bei Funktionen
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Bestimme, welche Symmetrie beim Graphen vorliegt.
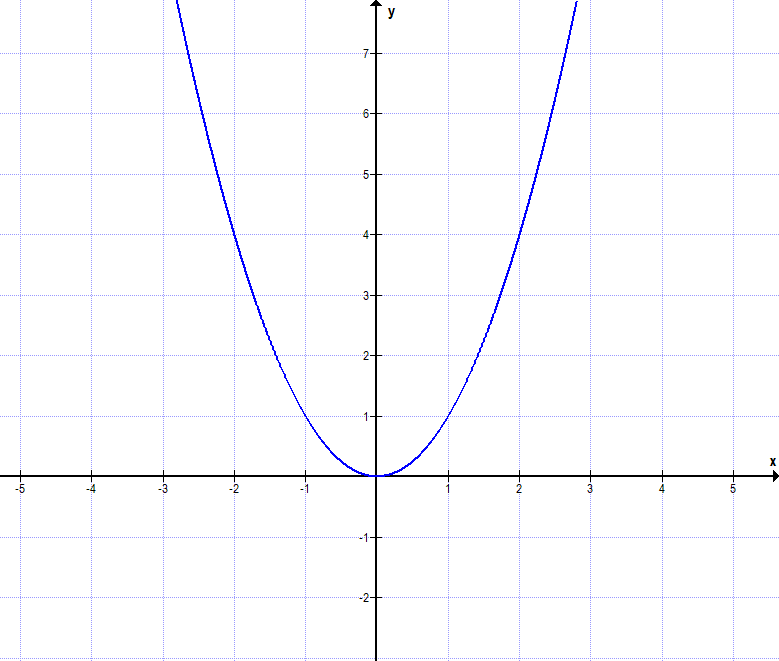
Dies ist eine Parabel. Sie ist achsensymmetrisch (also Symmetrie zur y-Achse).
Die Funktionsgleichung lautet: f(x) = x².
Bestimme, welche Symmetrie beim Graphen vorliegt.
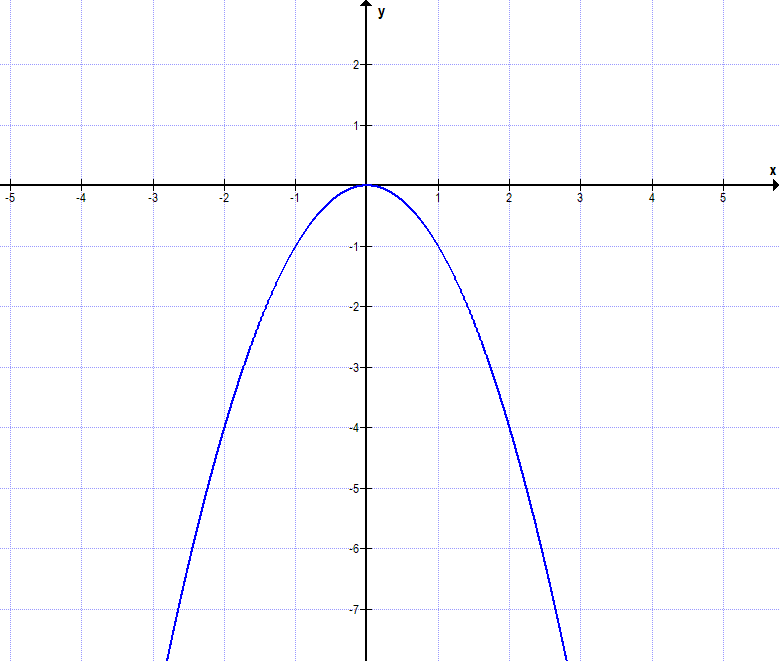
Dies ist eine Parabel, die nach unten geöffnet ist. Sie ist achsensymmetrisch (also Symmetrie zur y-Achse).
Die Funktionsgleichung lautet: f(x) = -x².
Bestimme, welche Symmetrie beim Graphen vorliegt.
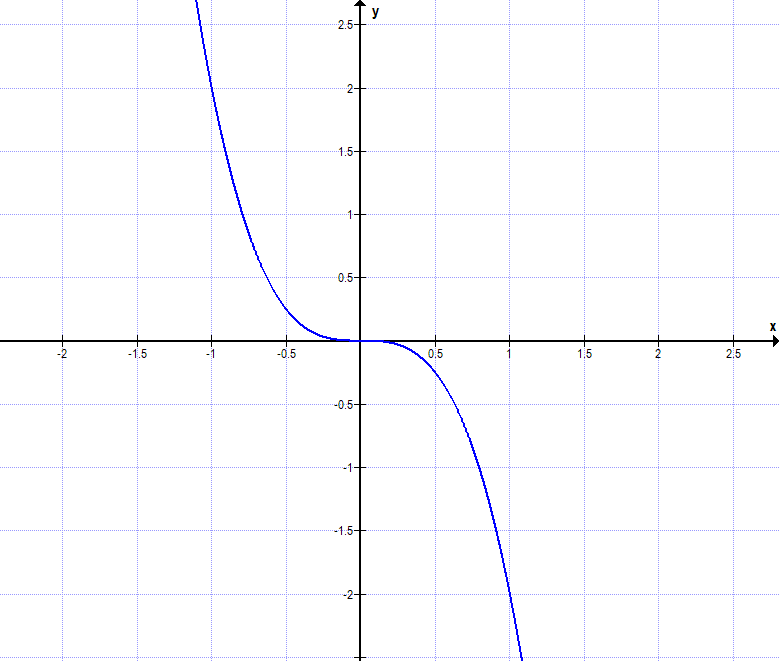
Dies ist der Graph der Funktion f(x) = 2x3. Er ist punktsymmetrisch zum Koordinatenursprung.
Bestimme, welche Symmetrie vorliegt: f(x) = x4 + 3·x2 + 2
Es liegt Achsensymmetrie vor, da es sich um eine gerade Funktion handelt. Das heißt, die Funktionsgleichung beinhaltet nur gerade Exponenten.
Bestimme, welche Symmetrie vorliegt: f(x) = x7 + 0.5·x3
Es liegt Punktsymmetrie vor, da es sich um eine ungerade Funktion handelt. Das heißt, die Funktionsgleichung beinhaltet nur ungerade Exponenten.
Fortschritt:
