CHECK: Wurzeln (schwierig) I
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Was ist die Quersumme von 123456?
Für die Quersumme addieren wir alle Ziffern: 1+2+3+4+5+6 = 21
Die Wurzel aus 441 ist 21, also ist √441 die korrekte Antwort.
Was ist die Wurzel aus x²?
Beispiel mit 5: √(5²) = √25 = 5
Beispiel mit -5: √((-5)²) = √25 = 5
Es muss also immer der „Startwert“, nur ohne Minus-Vorzeichen, erhalten werden.
Diese Verknüpfung heißt Betrag von x oder |x|.
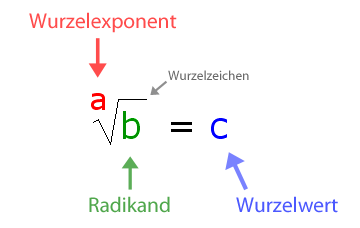
Wie heißt die Zahl unter dem Wurzelzeichen mit ihrem Fachbegriff?
Der Radikand befindet sich unter dem Wurzelzeichen.
Gib die 3-te Wurzel aus \( z^{-27} \) an und vereinfache weitmöglichst.
\( \sqrt[3]{z^{-27}} = (z^{-27})^{\frac{1}{3}} = z^{-\frac{27}{3}} = z^{-9} \)
Vereinfache die Wurzel so weit wie möglich: \( \sqrt[5]{ \sqrt[3]{32} } \)
5√(3√32) = (321/3)1/5 = 321/3·1/5 = (321/5)1/3 = 3√ (5√32) = 3√2
Gib die 5-te Wurzel aus \( a^{-15} \) an und vereinfache weitmöglichst.
\( \sqrt[5]{a^{-15}} = (a^{-15})^{\frac{1}{5}} = a^{-\frac{15}{5}} = a^{-3} \)
Gib alle Lösungen/Vereinfachungen von √4 an.
x² = 4 hätte in der Tat die Lösung x1 = -2 und x2 = 2. Wenn man aber die Wurzel aus 4 zieht, dann hat man nur das Ergebnis 2. Die -2 ist keine Vereinfachung.
Berechne das Produkt aus \( \sqrt[4]{6} · \sqrt[3]{6} \)
61/4·61/3 = 61/4+1/3 = 63/12+4/12 = 67/12
Wie wandelt man allgemein \( \sqrt[a]{x^b} \) in die Potenzschreibweise um?
\( \sqrt[a]{x^b} = x^{\frac{b}{a}}\)
Markiere das Wurzelgesetz zur Multiplikation zweier Wurzeln.
\( \sqrt[n]{x} · \sqrt[n]{y} = \sqrt[n]{x · y} \)
Fortschritt:
