CHECK: Knobelaufgaben II
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Drei Kirchturmuhren
Drei Kirchturmuhren schlagen gleichzeitig 12. Die eine Uhr geht richtig, die zweite Uhr geht jeden Tag 10 Minuten vor, die dritte Uhr geht täglich 12 Minuten nach.
Nach wieviel Tagen werden die drei Uhren wieder gleichzeitig 12 schlagen?
Die zweite Uhr geht nach 6 Tagen genau 1 h vor, d.h. nach 6·12 = 72 Tagen zeigt sie gleichzeitig mit der ersten Uhr 12:00 an.
Die dritte Uhr geht nach 5 Tagen genau 1 h nach, d.h. nach 5·12 = 60 Tagen zeigt sie gleichzeitig mit der ersten Uhr 12:00 an.
Um zu berechnen, wann alle 3 Uhren gleichzeitig wieder 12:00 anzeigen, sucht man das kgV von 60 und 72. Das ist gerade 360.
Geld zum Fenster hinauswerfen
Ein König hinterließ seinem Sohn 5000500 Goldtaler. Der Prinz, der schon sehr reich war und sich langweilte, beschloss, dieses Geld zum Zeitvertreib zum Fenster hinauszuwerfen.
Um einen Taler zu greifen, ihn hinauszuwerfen und die Hand wieder zurückzuziehen, brauchte der Prinz 2 Sekunden.
Wie lange müsste der Prinz täglich Geld zum Fenster hinauswerfen, wenn sein ganzes Erbe nach einem Jahr (365 Tagen) hinausgeworfen sein soll?
Jeden Tag muss der Prinz 5000500 : 365 = 13700 Taler hinauswerfen. Dazu braucht er 27400 Sekunden.
Das sind exakt 7 Stunden, 36 Minuten und 40 Sekunden.
Gewicht von Arnes Bruder
Arne fragt seinen Bruder, wie viel er wiegt. Die Antwort: "Ich wiege 10 kg und nochmals die Hälfte meines Gewichts".
Wieviel wiegt der Bruder?
20 kg = 10 kg + 20 kg : 2
Herzschläge eines Zehnjährigen
Das Herz eines Menschen schlägt in jeder Stunde durchschnittlich 4200 Mal.
Wie oft hat Jonas Herz genau 10 Jahre nach seiner Geburt geschlagen, wenn es in dieser Zeit genau 2 Schaltjahre gab?
10 normale Jahre haben 10 · 365 · 24 = 87 600 Stunden. Bei 2 Schaltjahren kommen noch 48 Stunden dazu. Es sind also nach Jonas Geburt genau 87 648 Stunden vergangen. In dieser Zeit schlug Jonas Herz 4200 · 87648 = 368 121 600 Mal.
Känguru Knut ist davongehüpft
Känguru Knut ist seiner Mutter davongehüpft. Es ist jetzt schon 150 Meter entfernt. Die Mutter hüpft Knut hinterher, während Knut weiterhüpft.
Knut macht immer 50 cm weite Sprünge. Immer wenn Knut einen Sprung macht, macht die Mutter einen 3 m weiten Sprung.
Nach wie vielen Sprüngen holt die Mutter Knut ein?
Bei jedem Sprung verringert sich der Abstand zwischen der Mutter und Knut um 250 cm. Da sie anfangs 15 000 cm voneinander entfernt waren, braucht die Mutter 15 000 cm : 250 cm = 60 Sprünge.
Eine Museumsführung
An einer Führung durch das Technikmusum nehmen 30 Personen teil und bezahlen zusammen 40 Euro. Der Eintritt kostet für Erwachsene je 2 Euro, für Rentner je 1,50 Euro und für Kinder je 1 Euro. Wenn es doppelt so viele Kinder wie Rentner sind. Wie viele Erwachsene nehmen dann an der Führung teil?
An dem Museumsbesuch nehmen 6 Erwachsene, 8 Rentner und 16 Kinder teil.
Lösung mit Hilfe eines Gleichungssystems:
(1) x + y + z = 30 (Anzahl der Personen)
(2) 2·x + 1,5·y + z = 40 (Eintrittspreise)
(3) 2·y = z (doppelt so viele Rentner wie Kinder)
Das LGS lösen wir mit Hilfe vom LGS Pro Rechner.
Die Lösungen lauten:
x = 6
y = 8
z = 16
Spezielle Zahlenmauer
Die Zahl 11 im grauen Kästchen ergibt sich aus der Regel 11 = 2·3 + 2 + 3:
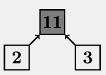
Welche Zahl muss nach der gleichen Regel in dem grauen Kästchen in folgender Zeichnung stehen?
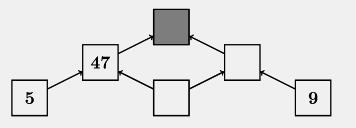
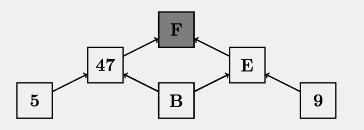
Wenn B, E und F die Zahlen in den freien Kästchen sind, so gilt für B nach der Regel B = (45-7) : 6 = 7. Damit folgt für E: E = 7·9 + 7 + 9 = 79 und für die gesuchte Zahl F: F = 47·79 + 47 + 79 = 3 839
Alles mit 3. Wir zerlegen die Zahlen.
Es seien a, b, c und d vier natürliche Zahlen, für die a + 3 = b - 3 = c·3 = d:3 gilt. Welches kann dann nicht die Summe a + b + c + d sein?
Wir formen alle Gleichungen nach c um:
a = 3 · c - 3
b = 3 · c + 3
d = 9 · c
Daher gilt für die Summe s = a + b + c + d = 3·c - 3 + 3·c + 3 + 3·c + 9·c = 18·c. Die Summe muss also durch 18 teilbar sein. Das trifft auf alle Zahlen außer 348 zu.
Munterer Pralinentausch
Anna, Beate und Charlotte haben jede eine bestimmte Anzahl Pralinen. Anna gibt Beate und Charlotte von ihren Pralinen so viele ab, wie diese jeweils schon haben. Danach gibt Beate Anna und Charlotte von ihren Pralinen so viele, wie diese jetzt haben. Schließlich gibt Charlotte Anna und Beate von ihren so viele Pralinen, wie diese inzwischen haben. Nun haben alle drei je 8 Pralinen. Wie viele Pralinen hatten die Mädchen vor dem Tausch?
Man kann die Tauschaktion nachspielen. Bei "Anna 13, Beate 7, Charlotte 4" geht es auf.
Bei den anderen Aufteilungen ist es entweder nicht möglich, alle 3 Tauschschritte zu machen oder es endet nicht bei 8.
Drei vertauschte Deckel
Auf einem Tisch liegen drei Schachteln mit jeweils zwei Kugeln. Eine Schachtel enthält zwei weiße Kugeln, eine zwei schwarze und eine je eine weiße und eine schwarze Kugel. Leider hat jemand die Deckel so vertauscht, dass keine der Beschriftungen mehr stimmt. Aus welcher Schachtel muss man mit geschlossenen Augen eine Kugel ziehen, um anschließend sagen zu können, welche Schachtel welche Kugeln enthält?

Fall 1: ziehen einer weißen Kugel. Dann ist die Zuordnung folgende:
Deckel: ss | sw | ww
---------------------
Kugeln: sw | ww | ss
Fall 2: ziehen einer schwarzen Kugel. Dann ist die Zuordnung folgende:
Deckel: ss | sw | ww
---------------------
Kugeln: ww | ss | sw
Fortschritt:
