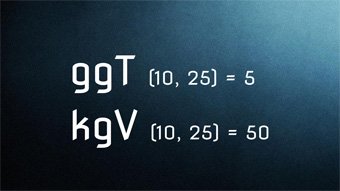Das kleinste gemeinsame Vielfache (kgV) gibt an, wann sich die Vielfachen von zwei Zahlen zum ersten Mal begegnen.
Zum Beispiel: kgV(6, 9) = 18
Die Vielfachen der Zahlen 6 und 9 „treffen“ sich das erste Mal bei 18.
Die 6 hat diese Vielfache: 6, 12, 18, 24, 30, 36, …
Die 9 aht diese Vielfache: 9, 18, 27, 36, 45, 54, …
Im Folgenden werden zwei Methoden vorgestellt, mit denen man das kgV bestimmen kann. Die Methoden ähneln denen zur Berechnung des ggT.