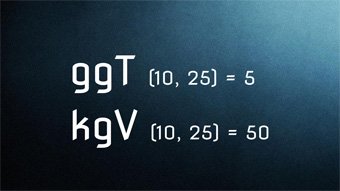Der größte gemeinsamer Teiler (ggT) gibt die größtmögliche Zahl an, durch die zwei oder mehrere Zahlen teilbar sind.
Zum Beispiel: ggT(30, 40) = 10
Die Zahlen 30 und 40 sind durch 10 teilbar (größtmöglicher Teiler). Sie wären auch durch 5 teilbar, jedoch ist 5 nicht der größtmögliche Teiler.
Im Folgenden werden zwei Methoden vorgestellt, mit denen man den ggT bestimmen kann.