AB: Lektion Lineare Funktionen - Einführung (Teil 2)
Berechne bzw. zeichne die Graphen, wenn gefordert.
Erstelle eine Wertetabelle für die Funktion f(x) = -2,5·x für die x-Werte 1, 2, 3 und 4.
| x | 1 | 2 | 3 | 4 |
| y | -2,5 | -5 | -7,5 | -10 |
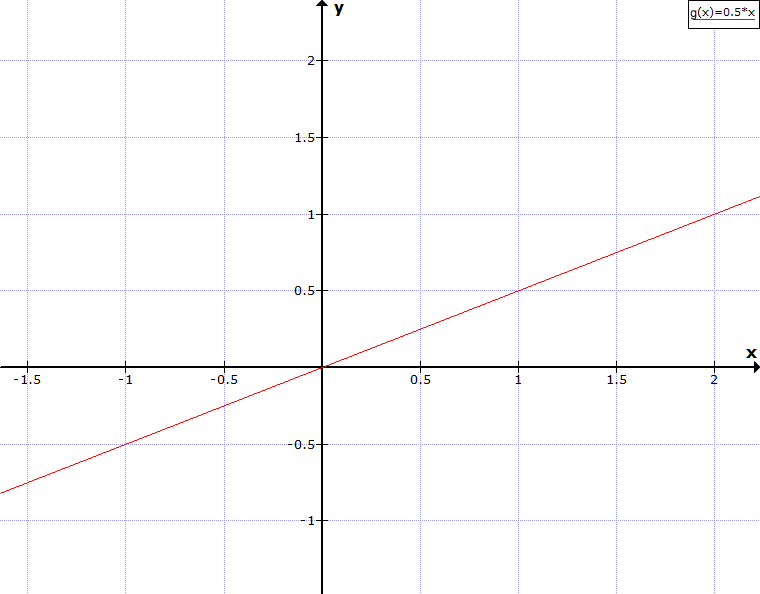
Zeichne den Graphen der Funktion g(x) = 0,5·x
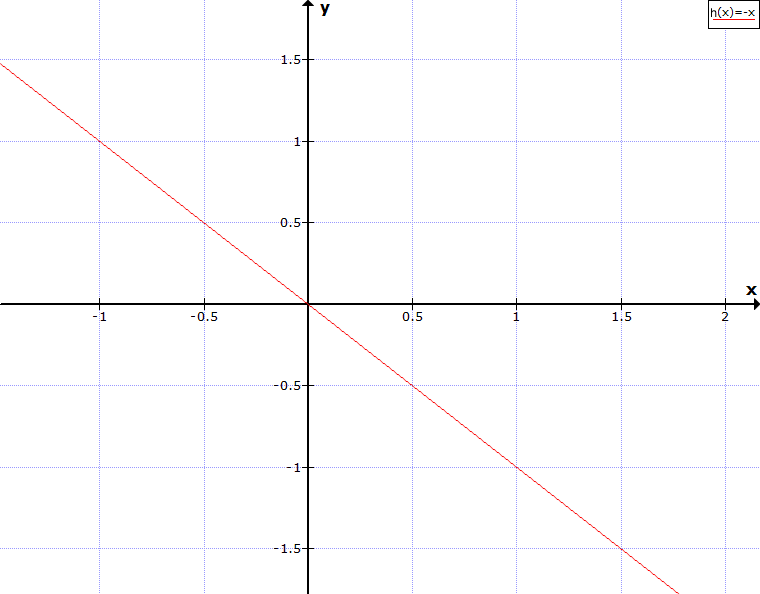
Zeichne den Graphen der Funktion h(x) = -x
Zeichne die Graphen k(x) = 2x und m(x)=x:2, was stellst du fest? Wie kannst du x:2 noch schreiben?
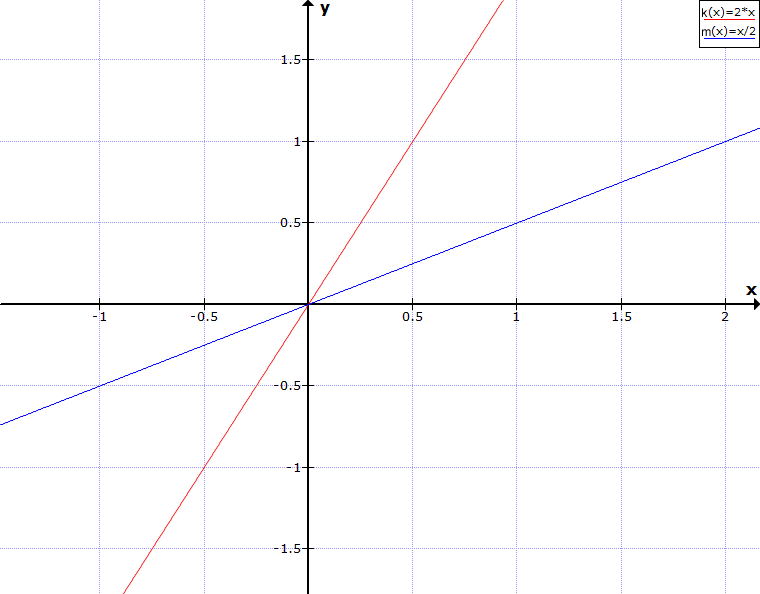
Die Division bei \( m(x) = x:2 \) kann als Bruch geschrieben werden, also \( m(x) = \frac{x}{2} \). Diesen Bruch kann man wie folgt umwandeln: \( \frac{x}{2} = \frac{1·x}{2} = \frac{1}{2}·x \), damit ergibt sich als Funktionsgleichung: \( m(x) = \frac{1}{2}·x \). Wir erkennen die Steigung mit \( \frac{1}{2} \) bzw. \( 0,5 \).
Zeichne den Graphen n(x) = 1,5·x und trage danach ein Steigungsdreieck ein. Wähle Koordinaten mit ganzen Zahlen.
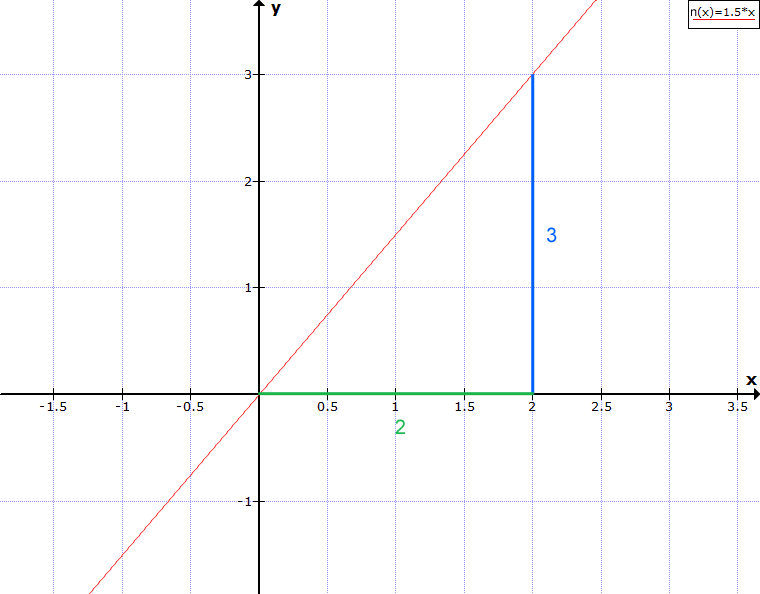
Das Steigungsdreieck hat die Höhe 3 und die Breite 2. Die Steigung kann man also auch als Bruch angeben: n(x) = 1,5·x wird zu \( n(x) = \frac{3}{2}·x \)
Zeichne den Graphen der Funktion p(x) = 2, was erkennst du?
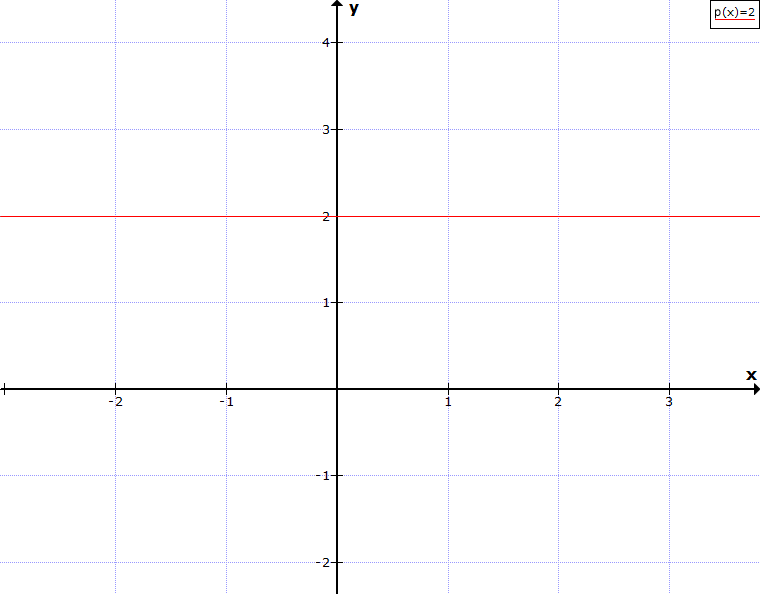
Wir erkennen, dass der Graph parallel zur x-Achse verläuft. Man spricht hier von einer konstanten (gleichbleibenden) Funktion, da jedem x-Wert immer der gleiche y-Wert 2 zugeordnet wird. Wählen wir ein paar Beispiel-Einsetzungen: p(x) = 2; p(1) = 2; p(2) = 2; p(3) = 2
Überlege, was passiert, wenn du bei einer Funktionsgleichung x=0 einsetzt, wo wird der Punkt immer sein?
Wenn du x=0 wählst, dann wirst du auf der x-Achse immer an der Stelle 0 sein. Die y-Achse geht durch die Stelle x=0 und alle Punkte auf der y-Achse haben die Stelle x=0. Mit anderen Worten, wenn wir x=0 setzen für einen Punkt(0|y), dann wird dieser Punkt stets auf der y-Achse liegen.
Überlege, was passiert, wenn du bei einer Funktionsgleichung y=0 wählst, wo wird der Punkt immer sein?
Wenn du y=0 wählst, dann wirst du auf der y-Achse immer die Höhe 0 haben. Die x-Achse geht durch die Höhe y=0 und alle Punkte auf der x-Achse haben die Höhe y=0. Mit anderen Worten, wenn wir y=0 setzen für einen Punkt(x|0), dann wird dieser Punkt stets auf der x-Achse liegen.
