AB: Lektion Lineare Funktionen - Einführung (Teil 3)
Graphen und Steigungen
Wie groß ist die Steigung bei der Funktion f(x) = 12·x?
Die Steigung beträgt 12. Die Steigung ist der Faktor an dem x.
Welche Steigung ist größer, die bei der Funktion a(x) = -x·5 oder bei b(x) = -x·(-5)?
Den Term -x·5 müssen wir umformen, um die Steigung ablesen zu können: -x·5 = -1·x·5 = -5·x. Auch die -x·(-5) müssen wir umformen: -x·(-5) = -1·x·(-5) = -1 ·(-5)·x = +5·x. Wie wir erkennen, ist die Steigung bei der Funktion b mit +5 größer als die Steigung bei der Funktion a mit (-5).
Welcher der Graphen stellt die Funktion f(x) = 2,5x dar?
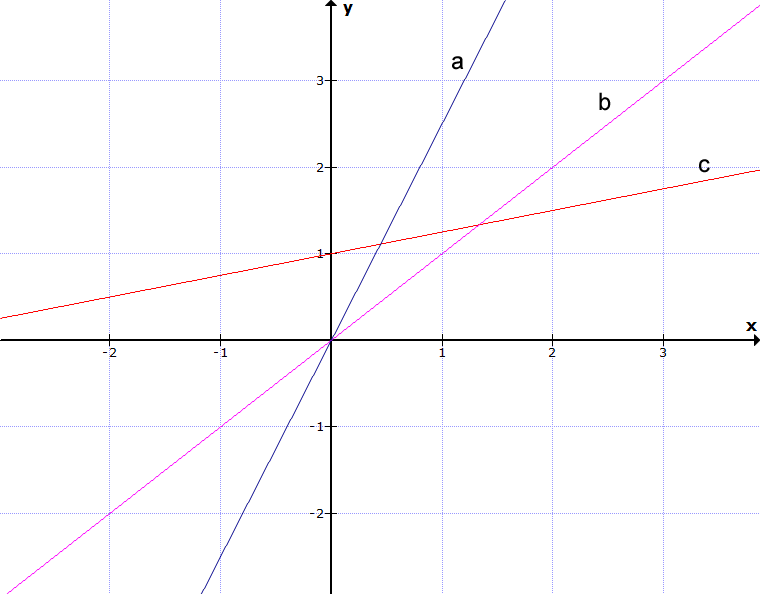
Es ist der Graph "a", denn er geht durch Ursprung und dann durch den Punkt (1|2,5). Daran können wir das Steigungsdreieck ablesen bzw. wir wissen, wir gehen 1 Einheit nach rechts und dann müssen wir 2,5 Einheiten nach oben gehen, um diesen Punkt zu erreichen. Die Steigung ist also 2,5.
Wie ergibt sich die Steigung, aus dem Verhältnis Differenz Breite / Differenz Höhe oder Differenz Höhe / Differenz Breite?
Die Steigung ergibt sich aus Differenz Höhe / Differenz Breite. Nehmen wir als Beispiel die Werte der vorigen Aufgabe, dort ist die Höhendifferenz = 2,5 und die Breitendifferenz = 1. Wir dividieren also Höhe : Breite = 2,5 : 1 und erhalten 2,5 als Steigung.
Welche Steigung hat die folgende Gerade?
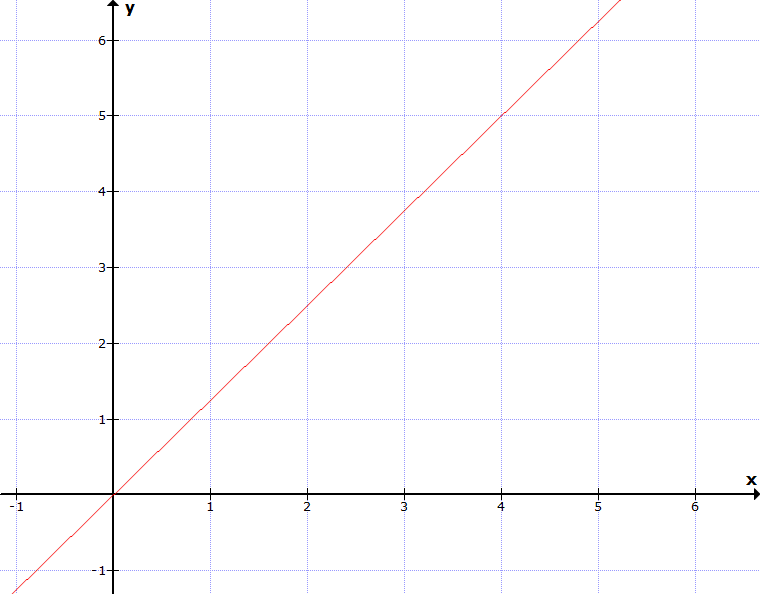
Die Gerade hat die Steigung 1,25. Das erkennen wir, wenn wir ein Steigungsdreieck einlegen, an ganze Werte P(0|0) und Q(4|5). Die Steigung ergibt sich mit 5:4 = 1,25.
Lies die Steigung der Geraden g und h ab. Wie lauten ihre Funktionsgleichungen?
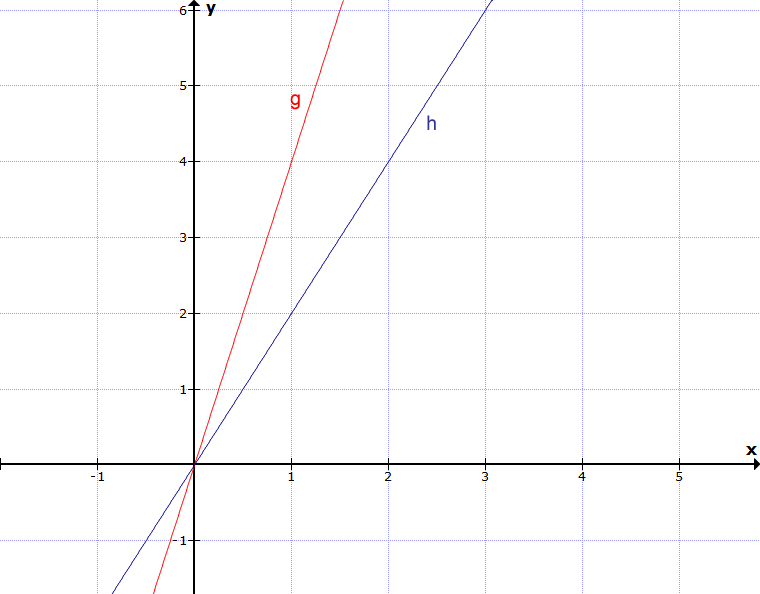
Beide Graphen gehen durch den Koordinatenursprung, die Funktionsgleichung hat also die Form f(x) = m·x (m ist hier eine Variable für die Steigung).
Beim Graphen g sehen wir, dass wir 1 Einheit nach rechts gehen und dann 4 Einheiten nach oben. Die Steigung beträgt also m = 4:1 = 4. Damit erhalten wir g(x) = 4·x.
Beim Graphen h sehen wir, dass wir 1 Einheit nach rechts gehen und dann 2 Einheiten nach oben. Die Steigung beträgt also m = 2:1 = 2. Damit erhalten wir h(x) = 2·x.
Wenn zwei Graphen parallel sind, siehe Grafik, was haben sie dann gemeinsam?
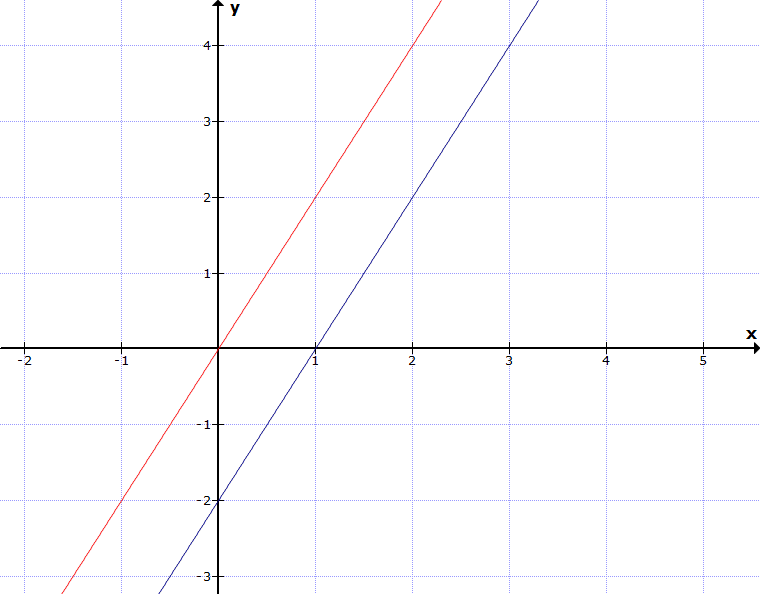
Die zwei Graphen haben die gleiche Steigung.
Welche Funktionsgleichung f(x)=3·x; g(x)=2·x; h(x)=-x passt zu folgendem Graphen:
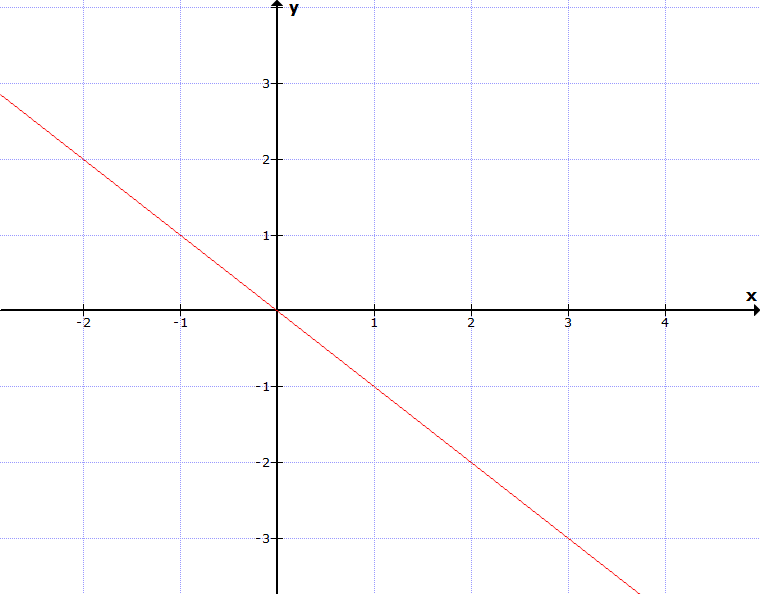
Der Graph verläuft nach unten, damit ist die Steigung negativ und die Funktion kann nur h(x) = -x sein.
