AB: Lektion Polynomfunktionen (ganzrationale Funktionen)
Nachfolgend findet ihr Aufgaben zu den Polynomfunktionen, mit denen ihr euer neues Wissen testen könnt.
Untersuche die folgenden Polynomfunktionen (ganzrationale Funktionen):
1. Gib den Grad der Funktion an und benenne den Leitkoeffizienten.
2. Ermittle die Schnittpunkte mit den Achsen.
3. Bestimme die Symmetrie (Punktsymmetrie zum Ursprung oder Achsensymmetrie zur y-Achse).
4. Führe eventuell eine Punktprobe durch.
5. Zeichne den Graphen der Funktion.
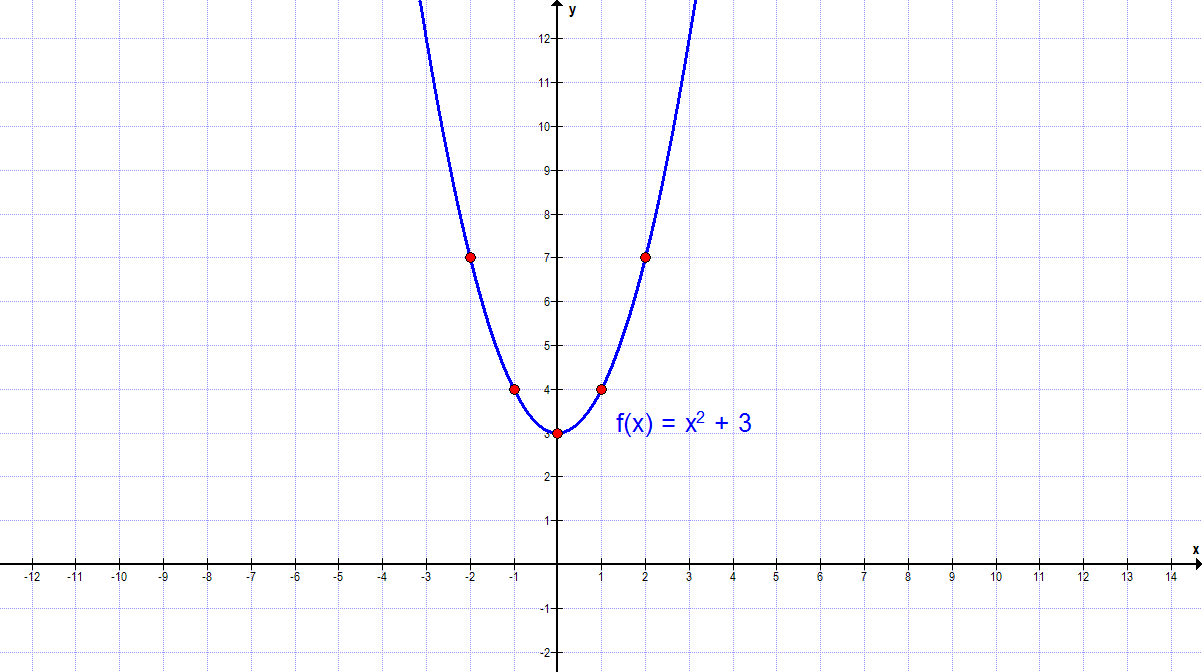
f(x) = x² + 3
f(x) = x² + 3
Gehen wir die Aufgabe der Reihenfolge nach an:
1. Der Grad der Funktion ist direkt mit 2 abzulesen. Der Leitkoeffizient ist 1, da auch der Vorfaktor von x² die 1 ist.
2. Der Schnittpunkt mit der y-Achse ist einfach bestimmt. Es ist x = 0 zu setzen. So erhalten wir f(x) = 0² + 3 = 3, also S(0|3). Dies war nicht anders zu erwarten, da uns das Absolutglied bereits als y-Achsenabschnitt bekannt ist.
Für die Schnittpunkte mit der x-Achse, also der Nullstellen, muss nun f(x) = 0 gesetzt werden.
f(x) = x² + 3 = 0 |-3
x² = -3
Es wird nie der Fall sein, dass x² negativ wird, wir haben also keine Lösung und damit auch keine Nullstellen.
3. Es liegen nur gerade Exponenten vor, damit handelt es sich um Achsensymmetrie.
4. Da kein Punkt gegeben ist, ist hier nichts zu tun.
5. Man kann die obigen Informationen zu Hilfe nehmen. Insbesondere die Informationen bezüglich der Schnittpunkte mit den Achsen, der etwaigen Punktprobe und die Symmetrie. Ist das nicht ausreichend, wird im Weiteren eine Wertetabelle aufgestellt. Für die Wertetabelle sind beliebige x-Werte zu wählen und die zugehörigen y-Werte auszurechnen. Die Wertetabellen seien hier nicht aufgezeigt, sie sind eigenständig aufzustellen.
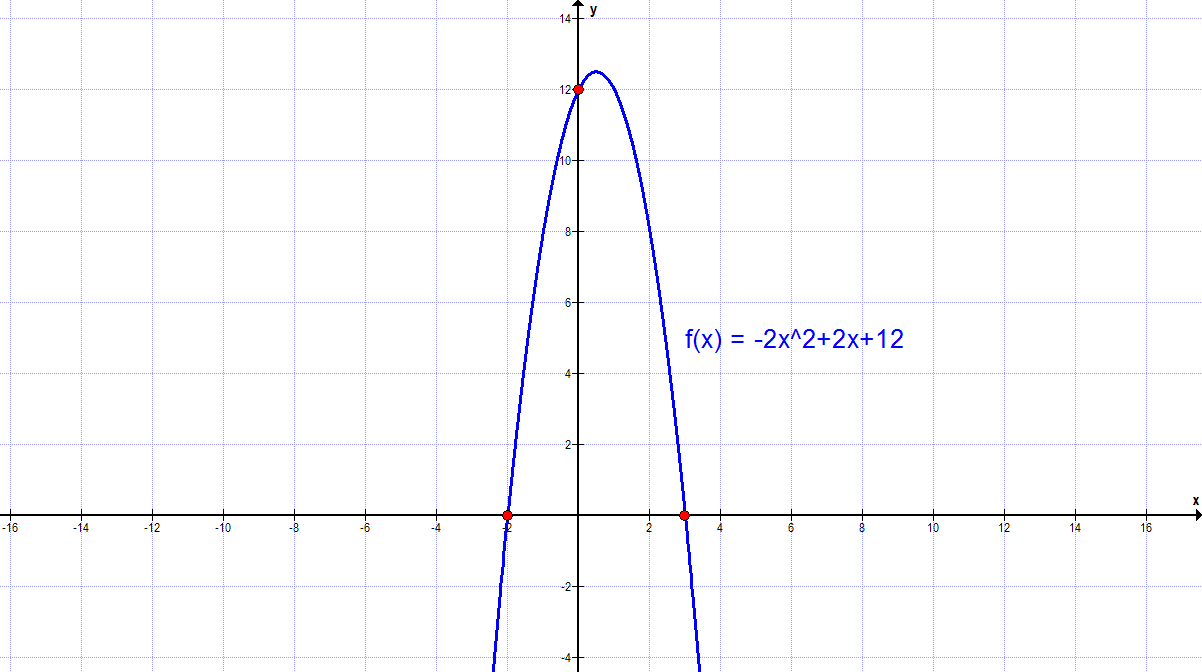
f(x) = 2x - 2x² + 12
Gehen wir die Aufgabe von vorne an:
Bevor wir beginnen, führen wir die Funktionsgleichung in die allgemeine Form über, also in erster Linie geordnet zu:
f(x) = -2x² + 2x + 12
1. Der Grad der Funktion ist direkt mit 2 abzulesen. Der Leitkoeffizient ist -2, da auch der Vorfaktor von x² die -2 ist.
2. Der Schnittpunkt mit der y-Achse ist einfach bestimmt. Es ist x = 0 zu setzen. Übrig bleibt f(x) = 12, also S(0|12).
Für die Schnittpunkte mit der x-Achse, also der Nullstellen, muss nun f(x) = 0 gesetzt werden.
f(x) = -2x² + 2x + 12 = 0
-2x² + 2x + 12 = 0 |:(-2)
x² - x - 6 = 0 |p-q-Formel mit p = -1 und q = -6
\( x_{1,2} = -( \frac{-1}{2} ) \pm \sqrt{ ( \frac{-1}{2} )^{2} - (-6)} \\ x_{1,2} = \frac{1}{2} \pm \sqrt{ \frac{1}{4} + 6} \\ x_{1,2} = 0,5 \pm \sqrt{6,25} \\ x_{1,2} = 0,5 \pm 2,5 \\ x_1 = 0,5 + 2,5 = 3 \\ x_2 = 0,5 - 2,5 = -2 \)
Die Nullstellen sind N1(-2|0) und N2(3|0).
3. Wir haben gerade und ungerade Exponenten vorliegen. Wir haben also keine der verlangten Symmetrien vorliegen.
4. Da kein Punkt gegeben ist, ist hier nichts zu tun.
5. Man kann die obigen Informationen zu Hilfe nehmen. Insbesondere die Informationen bezüglich der Schnittpunkte mit den Achsen, der etwaigen Punktprobe und die Symmetrie. Ist das nicht ausreichend, wird im Weiteren eine Wertetabelle aufgestellt. Für die Wertetabelle sind beliebige x-Werte zu wählen und die zugehörigen y-Werte auszurechnen. Die Wertetabellen seien hier nicht aufgezeigt, sie sind eigenständig aufzustellen.
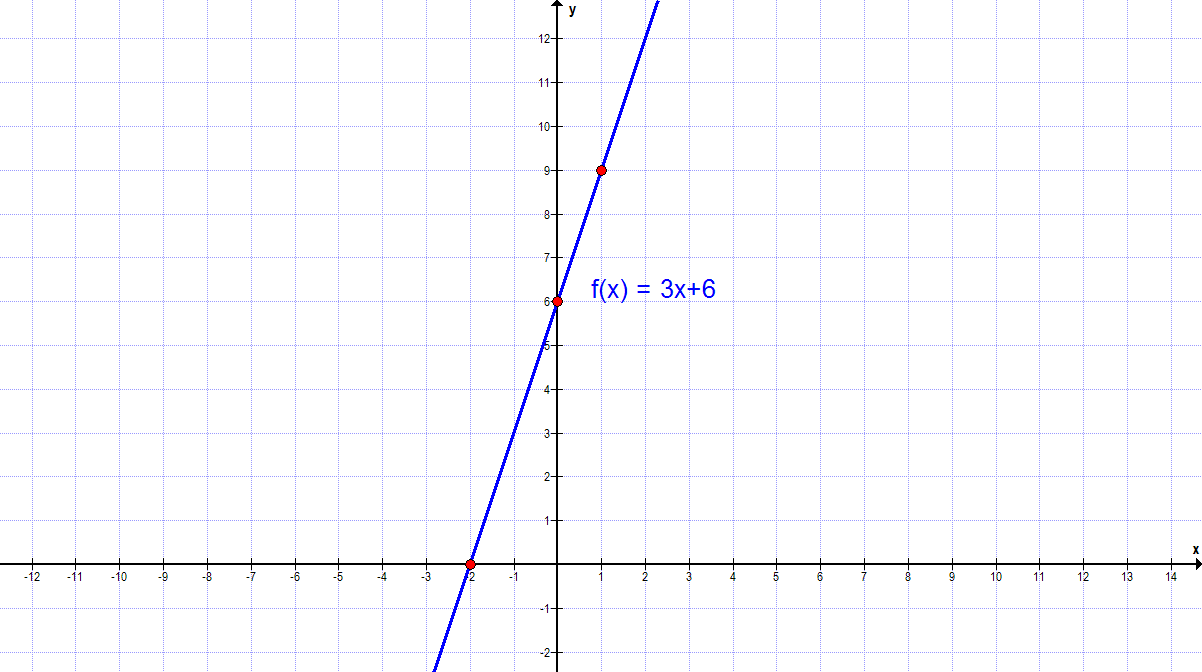
f(x) = 3x + 6 und A(1|8)
f(x) = 3x1 + 6
Gehen wir die Aufgabe von vorne an:
1. Der Grad der Funktion ist direkt mit 1 abzulesen. Der Leitkoeffizient ist 3, da auch der Vorfaktor von x die 3 ist.
2. Der Schnittpunkt mit der y-Achse ist einfach bestimmt. Es ist x = 0 zu setzen. Übrig bleibt f(x) = 6, also S(0|6).
Für die Schnittpunkte mit der x-Achse, also der Nullstellen, muss nun f(x) = 0 gesetzt werden.
f(x) = 3x + 6 = 0
3x + 6 = 0 |-6
3x = -6 |:3
x = -2
Die Nullstelle ist x = -2 und der Nullpunkt damit bei N(-2|0).
3. Wir haben hier eine Gerade. Diese ist punktsymmetrisch zu jedem ihrer Punkte. Da sie aber nicht durch den Ursprung geht (es ist ja S(0|6)), gibt es keine Punktsymmetrie zum Ursprung.
4. Eine Punktprobe wird beispielsweise so durchgeführt, dass der x-Wert in die Funktion eingesetzt wird und überprüft wird ob der errechnete und der angegebene y-Wert übereinstimmen. Das wäre hier x = 1 und y = 8.
Einsetzen:
f(1) = 3·1 + 6 = 9 ≠ 8
Der Punkt A liegt demnach nicht auf der Geraden.
5. Eine Gerade ist durch zwei Punkte bestimmt. Wir haben hier sogar 3 (nämlich S, N und B(1|9)). Damit ist das Zeichnen problemlos möglich:
f(x) = 3x² - x³ + 10x und A(1|12)
Gehen wir die Aufgabe von vorne an:
Bevor wir beginnen, überführen wir noch die Funktionsgleichung in die allgemeine Form über, also in erster Linie geordnet:
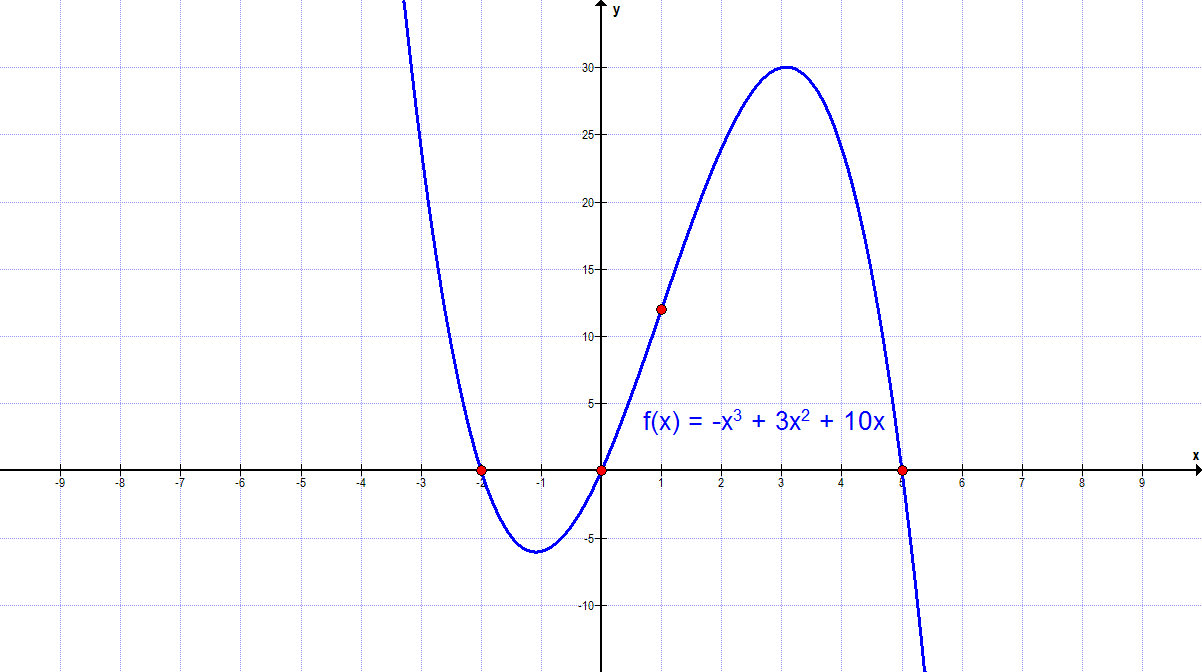
f(x) = -x³ + 3x² + 10x
1. Der Grad der Funktion ist direkt mit 3 abzulesen. Der Leitkoeffizient ist -1, da auch der Vorfaktor von x³ die -1 ist (-x³ = -1·x³).
2. Der Schnittpunkt mit der y-Achse ist einfach bestimmt. Es ist x = 0 zu setzen. Übrig bleibt f(x) = 0, also S(0|0).
Für die Schnittpunkte mit der x-Achse, also der Nullstellen, muss nun f(x) = 0 gesetzt werden.
f(x) = -x³ + 3x² + 10x = 0
-x³ + 3x² + 10x = 0
Nun gehen wir wie gelernt vor. Wir klammern -x aus. Denn dann können wir uns jeweils die Faktoren anschauen.
-x·(x² - 3x - 10) = 0
Wir erkennen also sofort am ersten Faktor, dass x1 = 0 sein soll. Weiterhin muss gelten x² - 3x - 10 = 0. Darauf die p-q-Formel angewendet mit p = -3 und q = -10.
\( x_{1,2} = -( \frac{-3}{2} ) \pm \sqrt{ ( \frac{-3}{2} )^{2} - (-10)} \\ x_{1,2} = \frac{3}{2} \pm \sqrt{ \frac{9}{4} + 10} \\ x_{1,2} = 1,5 \pm \sqrt{12,25} \\ x_{1,2} = 1,5 \pm 3,5 \\ x_1 = 1,5 + 3,5 = 5 \\ x_2 = 1,5 - 3,5 = -2 \)
Die Nullstellen sind also N1(0|0), N2(-2|0) und N3(5|0).
3. Wir haben gerade und ungerade Exponenten vorliegen. Keine Symmetrie.
4. Es wird der x-Wert von A(1|12) eingesetzt und überprüft, ob man auch den y-Wert enthält.
f(1) = -1³ + 3·1² + 10·1 = 12
Der Punkt A liegt folglich auf f(x).
5. Man kann die obigen Informationen zu Hilfe nehmen. Insbesondere die Informationen bezüglich der Schnittpunkte mit den Achsen, der etwaigen Punktprobe und die Symmetrie. Ist das nicht ausreichend, wird im Weiteren eine Wertetabelle aufgestellt. Für die Wertetabelle sind beliebige x-Werte zu wählen und die zugehörigen y-Werte auszurechnen. Die Wertetabellen seien hier nicht aufgezeigt, sie sind eigenständig aufzustellen.
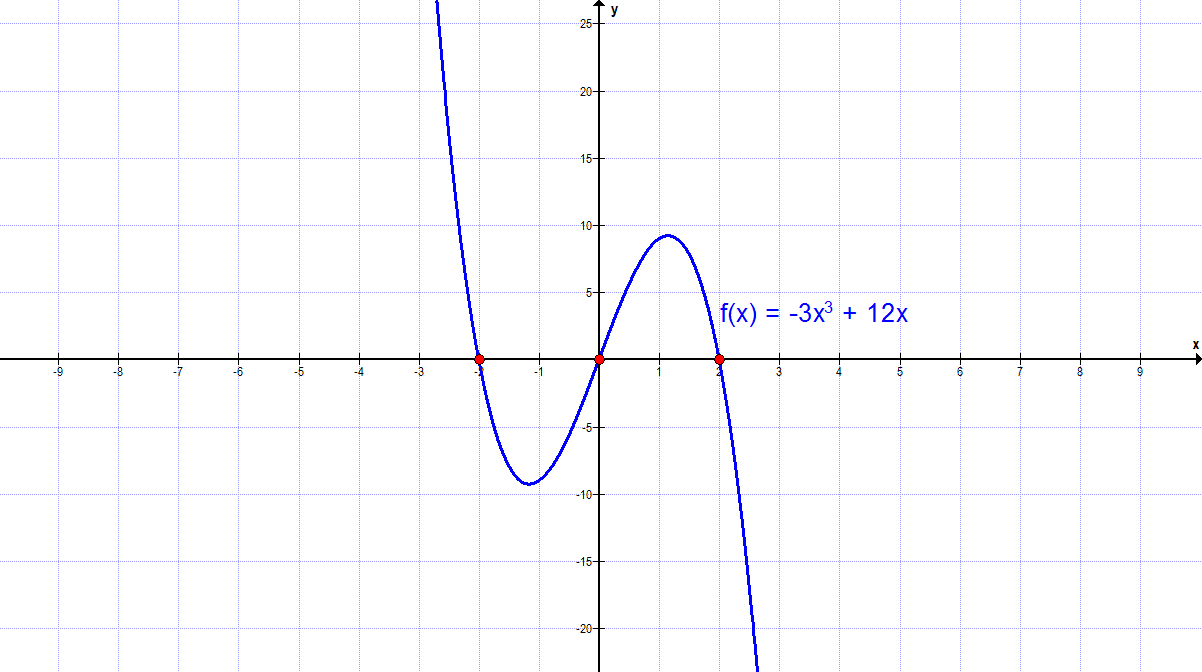
f(x) = -3x³ + 12x und A(0|0), B(2|7)
f(x) = -3x³ + 12x
Gehen wir die Aufgabe von vorne an:
1. Der Grad der Funktion ist direkt mit 3 abzulesen. Der Leitkoeffizient ist -3, da auch der Vorfaktor von x³ die -3 ist.
2. Der Schnittpunkt mit der y-Achse ist einfach bestimmt. Es ist x = 0 zu setzen. Übrig bleibt f(x) = 0, also S(0|0).
Für die Schnittpunkte mit der x-Achse, also der Nullstellen, muss nun f(x) = 0 gesetzt werden.
-3x³ + 12x = 0 |-3x ausklammern
-3x·(x²-4) = 0 |Dritte binomische Formel
-3x·(x+2)·(x-2) = 0
Die Nullstellen sind nun abzulesen. x1 = 0, x2 = -2
und x3 = 2. Damit sind die Nullpunkte N1(0|0),
N2(-2|0) und N3(2|0).
3. Wir haben nur ungerade Exponenten vorliegen. Wir haben also Punktsymmetrie zum Ursprung vorzuliegen.
4. Da A der Nullstelle N1 bzw. dem Schnittpunkt S entspricht, braucht es hier keine weitere Untersuchung. A liegt auf f(x). Für B gilt dasselbe. Es wurde bereits x3 = 2 bestimmt und als Nullstelle klassifiziert. B liegt also nicht auf f(x).
5. Man kann die obigen Informationen zu Hilfe nehmen. Insbesondere die Informationen bezüglich der Schnittpunkte mit den Achsen, der etwaigen Punktprobe und die Symmetrie. Ist das nicht ausreichend, wird im Weiteren eine Wertetabelle aufgestellt. Für die Wertetabelle sind beliebige x-Werte zu wählen und die zugehörigen y-Werte auszurechnen. Die Wertetabellen seien hier nicht aufgezeigt, sie sind eigenständig aufzustellen.