AB: Lektion Quadratische Funktionen (Teil 1)
Nachfolgend findet ihr Aufgaben zu den quadratischen Funktionen, mit denen ihr euer neues Wissen testen könnt.
Zeichne die Parabeln:
Um die Parabeln zu zeichnen, mag es hilfreich sein mit einer Wertetabelle zu arbeiten. Dafür einfach ein paar beliebige x-Werte nehmen (oft zwischen -5 und 5) und die passenden y-Werte dazu ausrechnen. Die so erhaltenen Punkte können dann in einen Graphen eingezeichnet werden und so entsteht letztlich unsere Parabel.
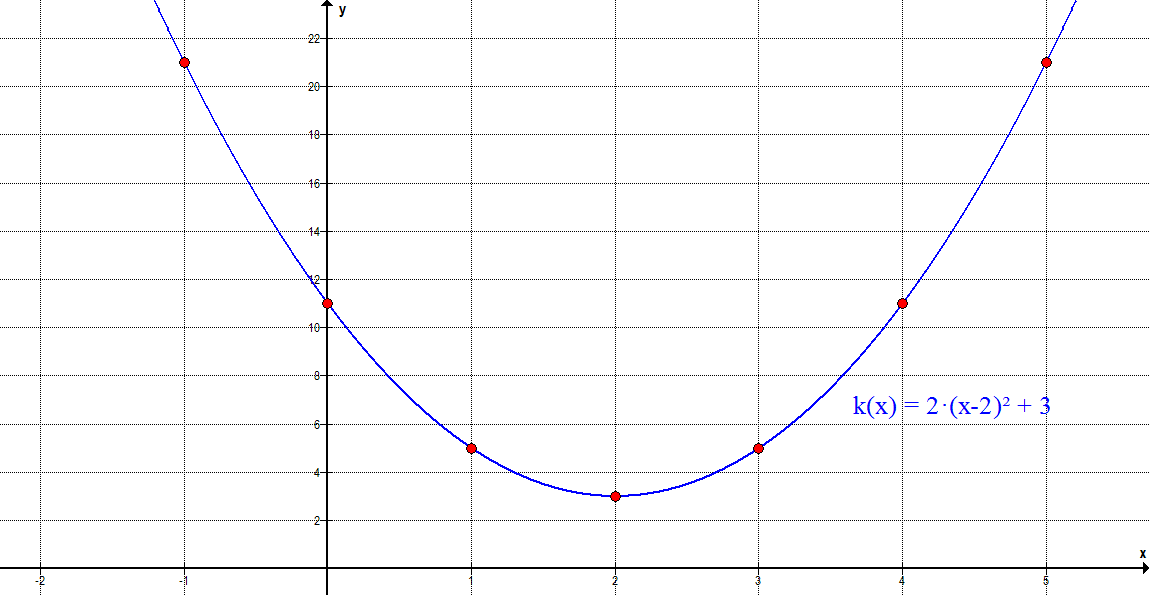
\( f(x) = \frac{1}{3} ·x^2 \)
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 16/3 | 3 | 4/3 | 1/3 | 0 | 1/3 | 4/3 | 3 | 16/3 |
Damit sieht der Graph wie folgt aus:
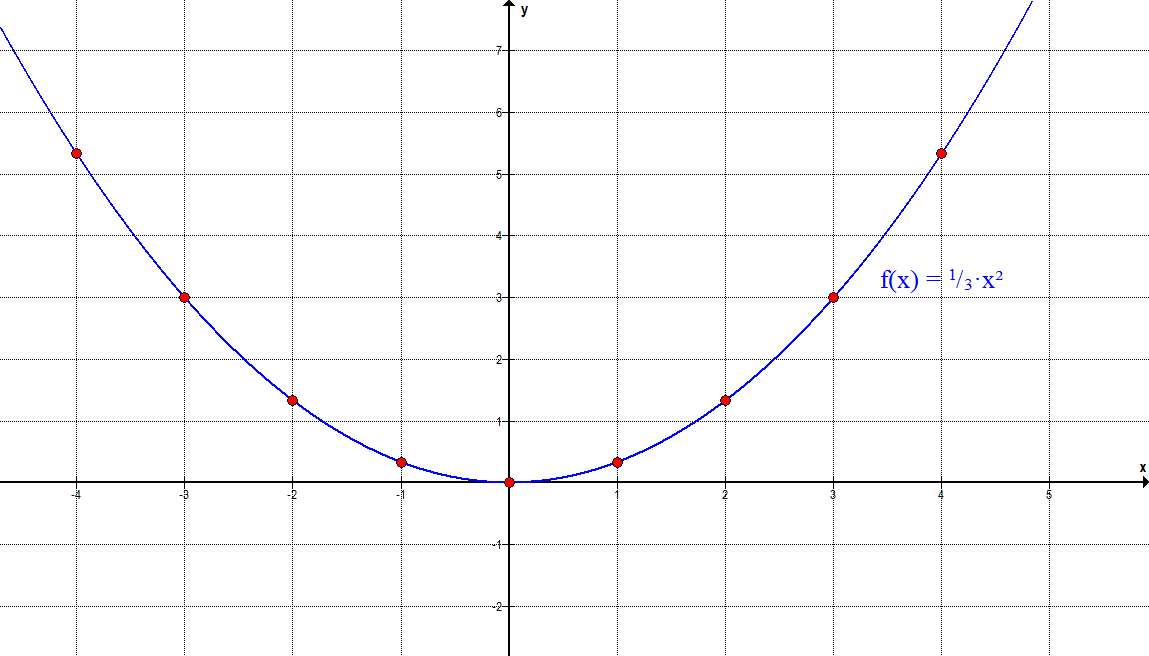
g(x) = 3·x² + 2
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 50 | 29 | 14 | 5 | 2 | 5 | 14 | 29 | 50 |
Damit sieht der Graph wie folgt aus:
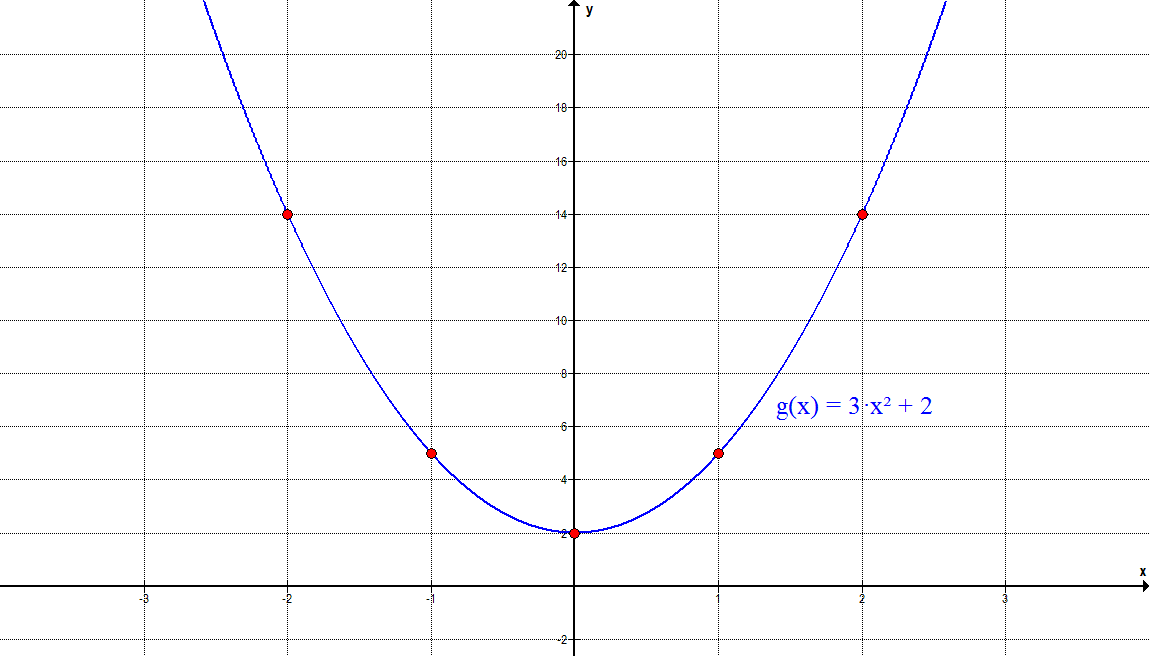
h(x) = 2·x² + 3·x + 1
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 21 | 10 | 3 | 0 | 1 | 6 | 15 | 28 | 45 |
Damit sieht der Graph wie folgt aus:
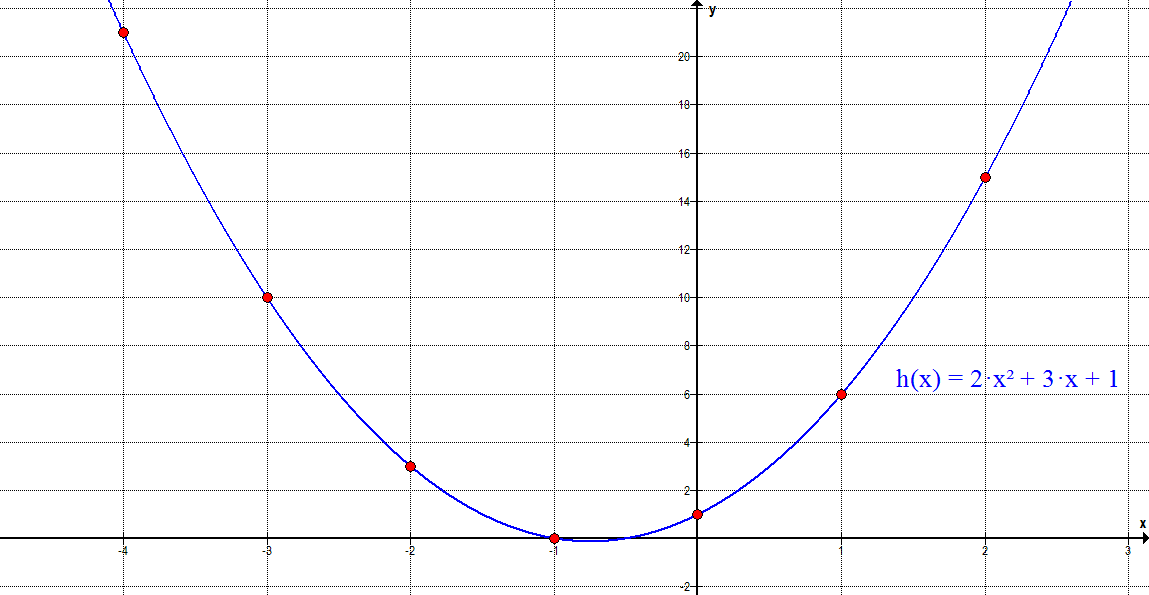
k(x) = 2·(x-2)² + 3
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 75 | 53 | 35 | 21 | 11 | 5 | 3 | 5 | 11 |
Damit sieht der Graph wie folgt aus: