Lektion G16: Antiproportionalität
In der letzten Lektion hatten wir uns die Proportionalität angeschaut. Jetzt ist deren Gegenstück, die Antiproportionalität bzw. indirekte Proportionalität, dran! Antiproportional meint: Erhöht sich ein Wert, so verringert sich ein anderer entsprechend im Verhältnis. Erfahrt Genaueres in dem folgenden Video.
Weitere Videos für Kunden:
-
G16-1 Antiproportionalität (Indirekte Proportionalität)Antiproportional bzw. indirekt proportional: Erhöht sich ein Wert so verringert sich ein anderer, verringert sich ein Wert, so erhöht sich ein anderer. Lösung über Antiproportionalitätsfaktor und Dreisatz.
Nachfolgend findet ihr Programme, mit denen ihr die Antiproportionalität besser verstehen bzw. euer bisheriges Wissen testen könnt.
-
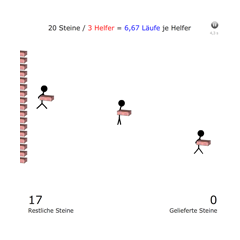 Antiproportionalität (Helfer)Erhöht ihr die Anzahl der Helfer, so verringert sich die Anzahl der Läufe, die für den Transport aller Steine notwendig ist. Der Antiproportionalitätsfaktor ist die Gesamtzahl der Ziegelsteine.
Antiproportionalität (Helfer)Erhöht ihr die Anzahl der Helfer, so verringert sich die Anzahl der Läufe, die für den Transport aller Steine notwendig ist. Der Antiproportionalitätsfaktor ist die Gesamtzahl der Ziegelsteine. -
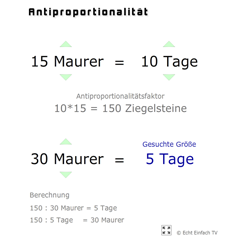 Antiproportionalität (Berechnung)Berechnet hier die gesuchte Größe über den Antiproportionalitätsfaktor (Maurer · Tage = Ziegelsteine).
Antiproportionalität (Berechnung)Berechnet hier die gesuchte Größe über den Antiproportionalitätsfaktor (Maurer · Tage = Ziegelsteine). -
 Antiproportionalitätsfaktor (als Fläche)Die Fläche ist der Antiproportionalitätsfaktor und stets konstant. Breite und Höhe verändern sich im gleichen (umgekehrten) Maße.
Antiproportionalitätsfaktor (als Fläche)Die Fläche ist der Antiproportionalitätsfaktor und stets konstant. Breite und Höhe verändern sich im gleichen (umgekehrten) Maße.
Hier findest du 1 Arbeitsblatt, mit dem du dein Wissen testen kannst.
Hier findest du 3 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.

