CHECK: Sinussatz I
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Was besagt der Sinussatz?
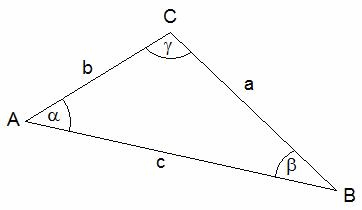
Der Sinussatz besagt: In jedem Dreieck verhalten sich die Längen zweier Seiten wie die Sinuswerte der gegenüberliegenden Winkel.
\( \frac {a} {sin(α)} = \frac {b} {sin(β)} = \frac {c} {sin(γ)} \)
Wann ist der Sinussatz in einem Dreieck unter anderem anwendbar?
Wenn zwei Seiten und ein Winkel gegeben sind, wobei der Winkel nicht von den zwei gegebenen Seiten eingeschlossen werden darf.
Berechne die fehlenden Seiten b und c im Dreieck mit Hilfe des Sinusatzes. Gegeben sind a = 5 cm und α = β = 45°.
Berechnung für Seite b:
Gemäß Sinussatz gilt hier:
\( \frac {a} {sin(α)} = \frac {b} {sin(β)} \)
Nach b aufgelöst
\( b = sin(β) \cdot \frac {a} {sin(α)} \)
Da α = β ist und deren Sinuswerte gleich sind, folgt
b = a
b = 5 cm
Berechnung für Seite c:
Mit dem Innenwinkelsummensatz lässt sich Winkel γ bestimmen:
α + β + γ = 180°
45° + 45° + γ = 180°
γ = 180° - 45° - 45°
γ = 90°.
Es handelt sich also um ein rechtwinkliges Dreieck, bei dem wir auch den Satz des Pythagoras anwenden könnten. Nun jedoch per Sinussatz:
$$ \frac {a} {sin(α)} = \frac {c} {sin(γ)} \\ \frac {5 cm} {sin(45°)} = \frac {c} {sin(90°)} \\ c = \frac {5 cm} {sin(45°)} \cdot \sin(90°) \\ c ≈ 7,0711 cm $$
Berechnungen siehe auch Sinussatz-Programm.
Berechne den gesuchten Winkel γ mit Hilfe des Sinussatzes. Gegeben sind a = 5 cm, c = 3 cm und α = 30°.

Nach dem Sinussatz gilt hier:
$$ \frac {a} {sin(α)} = \frac {c} {sin(γ)} $$
Nach dem Term sin(γ) umgestellt, ergibt
$$ sin(γ) = c\cdot \frac {sin(α)} {a} $$
Daraus ergibt sich der Winkel γ
$$ γ = arcsin(c\cdot \frac {sin(α)} {a}) $$
$$ γ = arcsin((3 cm)\cdot \frac {sin(60°)} {5 cm}) $$
$$ γ = arcsin(3 \cdot \frac {0,5} {5}) $$
$$ γ = arcsin (\frac {3} {10}) $$
γ ≈ 17,5°
Siehe auch Lösung im Sinussatz-Programm.
Berechne die gesuchte Seite b mit Hilfe des Sinussatzes. Gegeben sind a = 8 m, β = 75° und γ = 30°.

Nach dem Sinussatz gilt:
$$ \frac {a} {sin(α)} = \frac {b} {sin(β)} $$
Der Winkel β ist nicht gegeben, dafür der dritte Winkel im Dreieck namens γ.
Da die Innensumme aller Winkel im Dreieck 180° beträgt, kann man den Winkel α wie folgt berechnen:
α = 180° - β - γ = 180° - 75° - 30° = 75°
Da die Winkel α und β gleich groß sind, sind auch ihre Sinuswerte gleich groß.
Daraus folgt aus dem obigen Sinussatz a = b
→ b = 8 m
Fortschritt:
