CHECK: Sinussatz II
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Geometrische Bedeutung des Sinussatzes?
Der Sinussatz besagt, dass in jedem Dreieck die drei Verhältnisse „Seitenlänge dividiert durch Sinus des gegenüberliegenden Winkels“ gleich sind. Hat dies eine geometrischen Bedeutung?
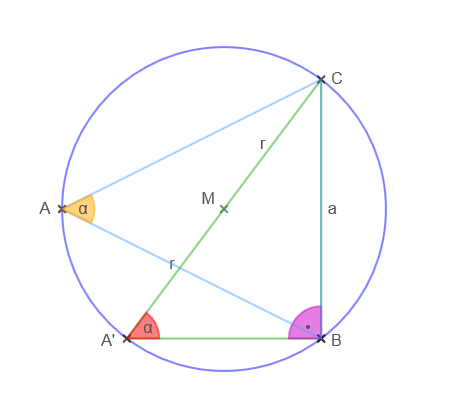
Unten ist das Dreieck ABC mit Umkreis, Radius r und Mittelpunkt M abgebildet. Die Dreiecksseite a ist eine Sehne des Umkreises, der Winkel α ist Umfangswinkel zur Sehne a. Alle Umfangswinkel zur Sehne a sind nach dem Umfangswinkelsatz gleich (auf der selben Seite des Kreises), also auch der rechte Winkel bei Punkt B. In diesem Fall verläuft die Strecke A'C durch den Mittelpunkt M des Umkreises (Satz des Thales) und es ist Strecke |A'C| = 2·r.
Im rechtwinkligen Dreieck A'BC gilt dann: sin(α) = a/(2·r)
und das kann man umstellen zu: a/sin(α) = 2·r
Bestimme die in der Skizze mit einer Linie dargestellte Breite des Flusses.
Bestimme die in der folgenden Skizze mit einer Linie dargestellte Breite des Flusses, wenn folgende Daten vorliegen.
Strecke BC = 100 m
Winkel ABC = 100 °
Winkel BCA = 20 °
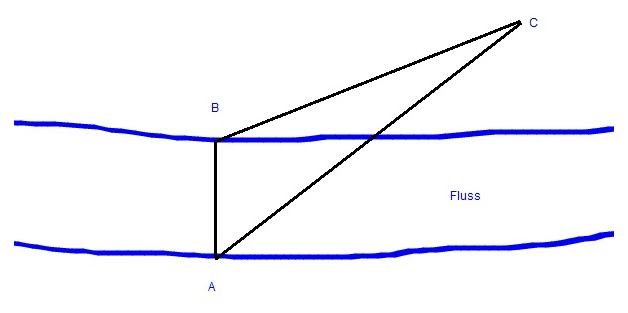
Sei die Flussbreite b.
Zunächst bestimmen wir den dritten noch unbekanten Winkel CAB:
$$ 180° = 100° + 20° +\angle CAB $$
$$ \angle CAB = 60° $$
Sinussatz:
$$ \frac {b} {sin(20°)} = \frac {\overline {BC}} {sin(60°)} $$
$$ b = sin(20°) \frac {\overline {BC}} {sin(60°)} $$
$$ b = sin(20°) \frac {100 \space m} {sin(60°)} $$
$$ b ≈ 39,5 m $$
Bestimme die Länge des Tunnels anhand der Skizze.
Um die Länge des geplanten Tunnels durch den Berg zu ermitteln, wurden vom Punkt C die Entfernung zum Punkt A und die Winkel α sowie γ vermessen:
a = 3 km, α = 30° und γ = 50°
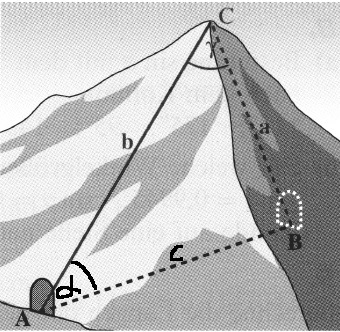
Laut Sinussatz:
$$ \frac c {sin(γ)}= \frac a {sin(α)} $$
$$ c = sin(γ)\frac a {sin(α)} $$
$$ c = sin(50°)\frac {3 \space km} {sin(30°)} $$
$$ c≈4,6 \space km $$
Fortschritt:
