CHECK: Vektorsubtraktion
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Subtrahiere die Vektoren (5|3) - (2|2).
\( \begin{pmatrix} 5 \\ 3 \end{pmatrix} - \begin{pmatrix} 2 \\ 2 \end{pmatrix} = \)
\( \begin{pmatrix} 5-2 \\ 3-2 \end{pmatrix}=\begin{pmatrix} 3 \\ 1 \end{pmatrix} \)
Subtrahiere die Vektoren (97|33) - (21|11).
\( \begin{pmatrix} 97 \\ 33 \end{pmatrix} - \begin{pmatrix} 21 \\ 11 \end{pmatrix} = \)
\( \begin{pmatrix} 97-21 \\ 33-11 \end{pmatrix} = \begin{pmatrix} 76 \\ 22 \end{pmatrix} \)
Wir möchten zwei Vektoren subtrahieren. Welche der Aussagen stimmt?
Genau wie bei der Vektoraddition subtrahieren wir die Vektoren komponentenweise.
Was benötigen wir, um die Subtraktion zweier Vektoren zu zeichnen?
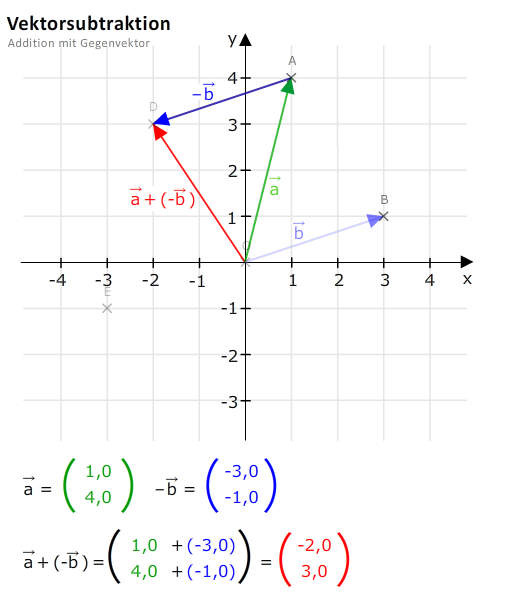
Wir zeichnen den Gegenvektor und verschieben ihn auf den Endpunkt des ersten Vektors.
Subtrahiere die Vektoren (0|5|5) - (2|6|5).
\( \begin{pmatrix} 0 \\ 5 \\ 5 \end{pmatrix} - \begin{pmatrix} 2 \\ 6 \\ 5 \end{pmatrix} = \)
\( \begin{pmatrix} 0-2 \\ 5-6 \\ 5-5 \end{pmatrix} = \begin{pmatrix} -2 \\ -1 \\ 0 \end{pmatrix} \)
Wie kann man den Nullvektor aus einem beliebigen Vektor \( \vec{a} \) erzeugen?
Wir erhalten den Nullvektor, wenn wir einen Vektor mit sich selbst subtrahieren.
\( \vec{a} - \vec{a} = 0 \)
Fortschritt:
