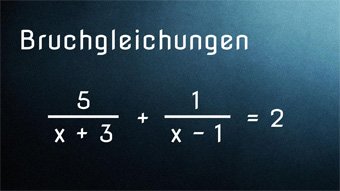Bruchgleichungen werden Gleichungen genannt, bei denen mindestens eine Unbekannte im Nenner eines Bruches auftritt.
Bruchgleichungen können wir eigentlich wie gewöhnliche Gleichungen lösen. Allerdings hat man die sogenannte Definitionsmenge zu berücksichtigen.
Definitionsmenge bedeutet nicht viel mehr als „was darf x für Werte annehmen“. Dazu müssen wir uns daran erinnern, dass es verboten ist (nicht definiert) durch 0 zu dividieren. Das heißt bei einem Bruch darf der Nenner nicht 0 werden.
Haben wir also eine Bruchgleichung gegeben, die beispielsweise die Gestalt:
$$ \frac{2}{3+x} + \frac{1}{x} = 5 $$
hat, so ist zu verhindern, dass keiner der Nenner den Wert 0 annimmt.
Dies wird durch die Definitionsmenge (man sagt auch „Definitionsbereich“) eingeschränkt und verdeutlicht.
Im obigen Fall haben wir dieses Problem, wenn der Nenner den Wert x = -3 oder den Wert x = 0 annimmt und so müssen diese mittels Festlegung der Definitionsmenge ausgeschlossen werden.
Das wird so geschrieben: D = ℝ \ {-3; 0}
Es bedeutet: Die Definitionsmenge beinhaltet alle reellen Zahlen ohne (das ist der Schrägstrich) die Zahlen -3 und 0.
Diese zusätzliche Vorüberlegung und Angabe ist bei Bruchgleichungen notwendig.
Außerdem ist zu beachten: Sollte sich als Ergebnis eine der nicht erlaubten Zahlen ergeben, so darf sie nicht als Lösung verwendet werden.