Es kann vorkommen, dass wir eine Zeichnung mit Angabe des Maßstabs vorzuliegen haben, wobei jedoch die Maßangaben fehlen. Zum Beispiel können in der Zeichnung die Längenangaben an Strecken fehlen.
Wenn die Zeichnung maßstabsgetreu ist, das heißt, alle Längen sind korrekt vergrößert worden, können wir die Längen der Strecken abmessen und mit Hilfe des vorgegebenen Maßstabs auf die Originalgröße zurückrechnen.
Vergrößerungsmaßstab
Haben wir eine vergrößerte Zeichnung eines Objektes und ist uns nur der Maßstab bekannt, so können wir die Längen der Strecken abmessen (mit dem Lineal) und mit Hilfe des vorgegebenen Maßstabs auf die Originalgröße zurückrechnen.
Zum Beispiel: Maßstab 5 : 1. Das heißt, 5 cm auf der Zeichnung entsprechen 1 cm in der Wirklichkeit.
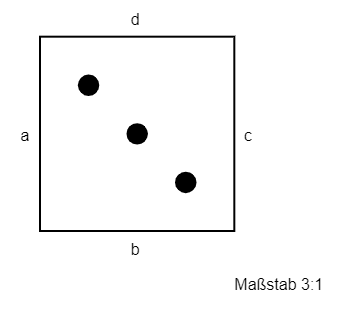
Im Folgenden haben wir ein Modell eines Würfels, das im Maßstab 3:1 gezeichnet wurde (in Seitenansicht).
Wir können nun mit dem Lineal die Längen der einzelnen Strecken (Seiten des Würfels) auf der Zeichnung abmessen. Wir erhalten:
- a = 6 cm
- b = 6 cm
- c = 6 cm
- d = 6 cm
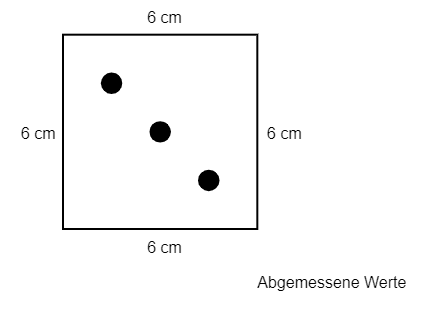
Tragen wir die abgemessenen Längen in die Zeichnung ein. Dies sind nicht die echten Kantenlängen des Würfels!
Jetzt wissen wir, dass der Maßstab 3:1 ist, damit können wir diese gemessenen Werte jetzt in die Originalgrößen umrechnen.
Dazu müssen wir einfach jeden Wert ·100 multiplizieren:
- a = 6 cm : 3 = 2 cm
- b = 6 cm : 3 = 2 cm
- c = 6 cm : 3 = 2 cm
- d = 6 cm : 3 = 2 cm
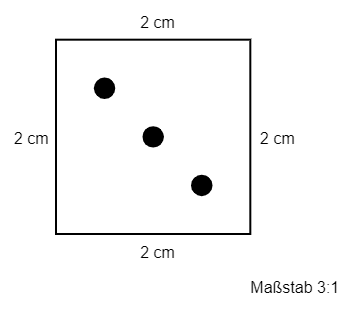
Dies sind die Originalgrößen, also die Längen der Würfelkanten in der Wirklichkeit. Sie sind 2 cm lang.
Nun können wir die Strecken in der Zeichnung entsprechend mit den Originalangaben beschriften, müssen aber auch den Maßstab dazu notieren.