In diesem Artikel geht es im Speziellen um das Taylorpolynom. Das Taylorpolynom ist ein Teil der Taylor-Formel, die vom Mathematiker Taylor Brook entwickelt wurde. Das Polynom dient zur Annäherung einer Funktion in der Umgebung eines Punktes.
Ziel des Verfahrens
Man möchte mit dem Taylorpolynom eine Funktion um einen bestimmten Punkt annähern. Das Ziel ist es, dass ein Polynom n-ten Grades entsteht.
Man kann mit Hilfe des Taylorpolynoms beispielsweise die trigonometrischen Funktionen Sinus und Kosinus annähern, für die es keine Polynomgleichung gibt.
Allgemeine Form des Taylorpolynoms
Die allgemeine Form des Taylorpolynoms lautet:
\( {T}_{n}f(x;a)=\frac{f(a)}{0!}+\frac{ {f}^{(1)}(a)}{1!}· (x-a)+\frac{ {f}^{(2)}(a)}{2!}· (x-a)^2+\frac{ {f}^{(3)}(a)}{3!}· (x-a)^3...\frac{ {f}^{(n)}(a)}{n!}· (x-a)^n \)
Erklärung: Wie funktioniert das Taylorpolynom?
Beim Taylorpolynom geht es darum, dass möglichst viele Ableitungen an einer Stelle a mit den Ableitungen des künftigen Polynoms übereinstimmen.
Zuerst wird die allgemeine Form ignoriert und versucht, es so zu lösen. Wenn man jetzt ein Polynom 4. Grades haben möchte, welches die Funktion cos(x) annähert, kann man wie folgt vorgehen:
Das künftige Polynom soll so aussehen:
\( {T}_{4}\cos(x)=ax^4+bx^3+cx^2+dx+e \)
Davon sind das die Ableitungen, die mit den Ableitungen von cos(x) übereinstimmen sollen. Jetzt muss man aber noch bestimmen, um welche Stelle a die Funktion angenährt werden soll. Für das Beispiel wird die Umgebung von 0 betrachtet. Also müssen die Ableitungen bei a = 0 übereinstimmen und natürlich auch die Ausgangsfunktion.
Dafür bildet man jeweils die Ableitungen des allgemeinen Polynoms und auch die der Ausgangsfunktion, da jene gleich sein müssen.
\( \begin{array}{lll} { {T}_{4} }^{(0)}\cos(x) & = a· x^4+b· x^3+c· x^2+d· x+e & = \cos(x) \\ { {T}_{4} }^{(1)}\cos(x) & = 4· a· {x}^{3}+3· b· x^2+2· c· x+d & = -\sin(x) \\ { {T}_{4} }^{(2)}\cos(x) & = 12· a· x^2+6· b· x+2· c & = -\cos(x) \\ { {T}_{4} }^{(3)}\cos(x) & = 24· a· x+6· b & = \sin(x) \\ { {T}_{4} }^{(4)}\cos(x) & = 24a & = \cos(x) \end{array} \)
Damit man mit den Variablen nicht durcheinander kommt, haben wir einfach x stehen lassen. Jetzt muss man dort a einsetzten und dann zu dem übrigen Koeffizienten auflösen:
\( \begin{array}{llll} a·0^4+b· 0^3+c· 0^2+d· 0+e & = \cos(0) & = 1 & ⇒ e=1 \\ 4·a· {0}^{3}+3· b· 0^2+2· c· 0+d & = -\sin(0) & = 0 & ⇒ d=0 \\ 12·a· 0^2+6· b· 0+2· c & = -\cos(0) & = -1 & ⇒ c=-\frac{1}{2} \\ 24·a· 0+6· b & = \sin(0) & = 0 & ⇒ b=0 \\ 24·a & = \cos(0) & = 1 & ⇒ a=\frac{1}{24} \end{array} \)
Das Taylorpolynom 4. Grades zu f(x) = cos(x) bei a = 0 ist also:
\( { {T}_{4} }\cos(x;0)=\frac{1}{24}· {x}^{4}-\frac{1}{2}· x^2+1 \)
Jetzt noch einmal die Überprüfung mit der allgemeinen Formel. Diese dürfte jetzt auch selbsterklärend sein:
\( {T}_{4}\cos(x;0)=\cos(1)-\sin(1)· (x-0)-\frac{\cos(1)}{2!}· (x-0)^2+\frac{\sin(0)}{3!} · (x-0)^3+\frac{cos(0)}{4!} · (x-0)^4 \\ {T}_{4}\cos(x;0)=1-0-\frac{1}{2} · t x^2+0+\frac{1}{14}· x^4 \\ {T}_{4}\cos(x;0)=\frac{1}{24}· x^4-\frac{1}{2}· x^2+1 \)
Beide Wege führen zum gleichen Ergebnis, nur geht es mit der zweiten Variante deutlich schneller. Kann man denn überhaupt so Funktionen näherungsweise als Polynom darstellen?
Vergleich der Graphen
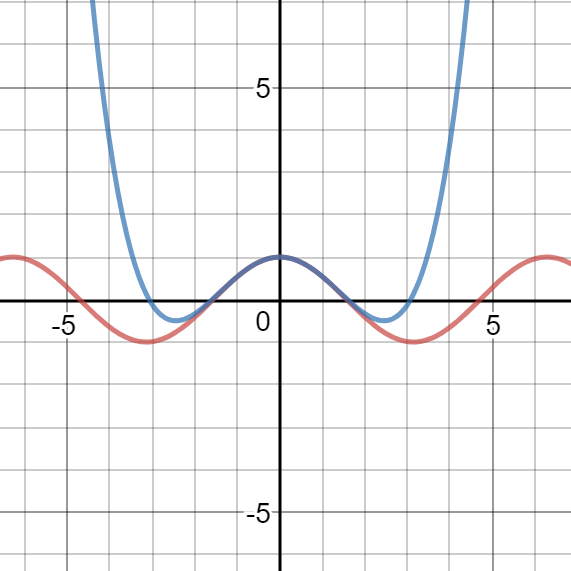
Der blaue Graph für das Polynom kommt der roten Ausgangsfunktion für Kosinus schon ziemlich nah.
Annäherung Graph Taylorpolynom an Sinuskurve
Nachstehend kann man die Annäherung eines Taylorpolynoms (Grad frei wählbar) an f(x) = sin(x) (also an die Sinuskurve) visualisieren:
Anwendungen des Taylorpolynoms
Jetzt stellt sich noch die Frage, wofür man das überhaupt braucht.
Für das Taylorpolynom gibt es viele verschiedene Anwendungen. Ein Beispiel hierfür ist das Ermitteln der Nullstellen von Exponentialfunktionen. Dafür muss man wissen, wo die Nullstellen sind. Dann kann man die Funktion näherungsweise mit einem Taylorpolynom nähern und eine genauere Stelle ausrechnen.
Eine andere Anwendung könnte sein, wenn man zwei Funktionen gleichsetzen möchte, die eine ist ein normales Polynom und die andere ist eine Exponentialfunktion. In dem Fall bringt man alles auf eine Seite, sodass 0 = Rest steht. Dann ersetzt man die Null durch eine Funktionsvorschrift, wie f(x) oder f: y = … und kann schließlich wie oben erläutert die Nullstellen bestimmen.
Taylorpolynom für Annäherung an tan(x) um Punkt x = 0 mit Grad 5
1. Zuerst bilden wir die allgemeine Form mit den Ableitungen:
\( \begin{array}{lll} f(x) & = a·x^5 + b·x^4 + c·x^3 + d·x^2 + e·x + f & = \tan(x) \\ f′(x) & = 5a·x^4 + 4b·x^3 + 3c·x^2 + 2d·x + e & = sec^2(x) \\ f′′(x) & = 20a·x^3 + 12b·x^2 + 6c·x + 2d & = 2·sec^2(x) · tan(x) \\ f′′′(x) & = 60a·x^2 + 24b·x + 6c & = 4·sec^2(x)·tan^2(x) + 2·sec^4(x) \\ f′′′′(x) & = 120a·x + 24b & = 8·sec^2(x) · tan^3(x) + 16·sec^4(x) · tan(x) \\ f^{\prime \prime \prime \prime \prime}(x) & = 120a & = 16·sec^2(x) · tan^4(x) + 88·sec^4(x) · tan^2(x) + 16·sec^6(x) \end{array} \)
2. Nun bestimmen wir das Polynom mit x = 0:
\( \begin{array}{llll} a·0^5 + b·0^4 + c·0^3 + d·0^2 + e·0 + f & = \tan(0) & = 0 \quad ⇒ & f = 0 \\ 5a·0^4 + 4b·0^3 + 3c·0^2 + 2d·0 + e & = sec^2(0) & = 1 \quad ⇒ & e = 1 \\ 20a·0^3 + 12b·0^2 + 6c·0 + 2d & = 2·sec^2(0) · tan(0) & = 0 \quad ⇒ & d = 0 \\ 60a·0^2 + 24b·0 + 6c & = 4·sec^2(0)·tan^2(0) + 2·sec^4(0) & = 2 \quad ⇒ & c = \frac{2}{6} = \frac{1}{3} \\ 120a·0 + 24b & = 8·sec^2(0) · tan^3(0) + 16·sec^4(0) · tan(0) & = 0 \quad ⇒ & b = 0 \\ 120a & = 16·sec^2(0) · tan^4(0) + 88·sec^4(0) · tan^2(0) + 16·sec^6(0) & = 16 \quad ⇒ & a = \frac{16}{120} = \frac{2}{15} \end{array} \)
3. Nun setzen wir die ermittelten Werte für a, b, c, d, e und f in unser Ausangspolynom ein:
f(x) = ax5 + b·x4 + c·x3 + d·x2 + e·x + f ≈ tan(x)
f(x) = \( \frac{2}{15} \)·x5 + 0·x4 + 2·x3 + 0·x2 + 1·x + 0 ≈ tan(x)
f(x) = \( \frac{2}{15} \)·x5 + \( \frac{1}{3} \)·x3 + 1·x ≈ tan(x)
4. Vergleich der Graphen – Polynomgraph gegenüber Tangensgraph:
~plot~ 2/15*x^5+2x^3+x;tan(x);[[-1.5|2.5|-4|4]];noinput ~plot~
Ergebnis: Wir haben den Tangens mit dem Polynom angenähert.
Taylorpolynom-Rechner
• eMathHelp Taylor and Maclaurin
• WolframAlpha Taylor Series
• Symbolab Taylor
• SolveMyMath Taylor Series Expansion
Weitere Artikel zum Thema:
• Reihenentwicklung nach Taylor
• Taylorreihe: Sinus konkret berechnen
