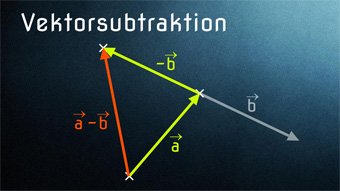
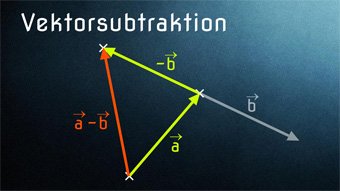
Nachdem wir uns die Vektoraddition angeschaut haben, wenden wir uns der Subtraktion von Vektoren zu. Diese ähnelt der Addition - wir führen sie sogar auf diese zurück.
Um eine Subtraktion in eine Addition umzuwandeln, können wir allgemein schreiben: a - b = a + (-b). Und genauso machen wir das bei den Vektoren. Es gilt die gleiche Regel:
\( \vec{a} - \vec{b} = \vec{a} + (-\vec{b}) \)
Das \( - \vec{b} \) ist dabei der Gegenvektor zu \( \vec{b} \).
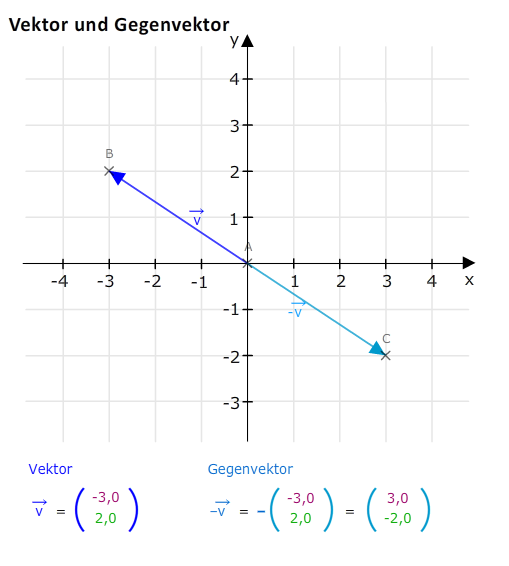
Gegenvektor bedeutet also nichts anderes, als dass der gleiche Vektor vorliegt, dessen Komponenten jedoch ein umgekehrtes Vorzeichen haben, was als Umkehrung der Richtung resultiert. Die Länge bleibt gleich.
\( \vec{v} = \begin{pmatrix} -3\\2 \end{pmatrix} \)
\( -\vec{v} = -\begin{pmatrix} -3\\2 \end{pmatrix} = \begin{pmatrix} 3\\-2 \end{pmatrix} \)
Betrachten wir eine Grafik, um uns das zu veranschaulichen. Zur Erinnerung: Vektoren kann man einzeichnen, wo man will, wichtig sind nur Länge und Richtung.
Die beiden abgebildeten Vektoren sind also abgesehen von der Richtung gleich, auch wenn sie nicht aufeinanderliegen.
Mit Hilfe des Gegenvektors können wir die Subtraktion nun wie eine Addition behandeln.
Nullvektor
Der Nullvektor muss definiert sein, damit wir ein Ergebnis erhalten, wenn wir einen Vektor mit sich selbst subtrahieren.
Also als Vektoren: \( \vec{a} - \vec{a} = \vec{o} \)