AB: Anwendung Integralrechnung II
Nachfolgend findet ihr Anwendungsaufgaben zur Integralrechnung im Alltag, mit denen ihr euer Wissen testen könnt.
Auf einer Seite einer Burg soll ein Burggraben ausgehoben werden. Er hat die Form einer Parabel. Er ist 6 Meter tief, 4 Meter breit und 25 Meter lang. Wie viel m³ Erde muss dafür abgetragen werden?
Um das Volumen zu berechnen, brauchen wir die Grundfläche (hier der Querschnitt, also die Parabel) und multiplizieren diesen mit der Länge. Um die Parabel zu berechnen, wählen wir ein geschicktes Koordinatensystem. Es bietet sich an den Boden also y = 0 zu wählen und damit haben wir den Tiefpunkt bei y = -6.
Die allgemeine Form einer Parabel lautet:
\( f(x) = a·x^2 + b·x + c \)
Da wir den Scheitelpunkt auf die y-Achse gelegt haben und die Parabel daher symmetrisch liegt, können wir direkt b = 0 (Symmetrie) und c = -6 (y-Achsenabschnitt) bestimmen. Bleibt a, welches wir durch die Breite erhalten. Diese ist ja A(-2|0) bzw B(2|0), also eine Gesamtbreite von 4. Wegen der Symmetrie schauen wir uns nur B an:
\( 0 = a · 2^2 + 0 · 2 - 6 \\ a = \frac{6}{4} = \frac{3}{2} \)
Unsere Parabel lautet demnach:
\( f(x) = \frac{3}{2}·x^2 - 6 \)
Die Grundfläche/Querschnittsfläche ergibt sich mit der Integralrechnung:
\( \int \limits_{-2}^2 \frac{3}{2}·x^2 - 6 \; dx \\ = \left[ \frac{1}{2}·x^3 - 6·x \right]^{2}_{-2} \\ = -16 \)
Eine Fläche ist stets positiv, wir haben also \( 16 \text{ m}^2 \) als Grundfläche. Das Volumen ergibt sich somit zu:
\( V = 16 \text{ m}^2 · 25 \text{ m} = 400 \text{ m}^3 \)
Es werden 400 m³ abgetragen.
Eine Badewanne ist zu Beginn leer und gestöpselt. 5 Sekunden lang fließt Wasser über den Wasserhahn. Die Menge ist dabei linear ansteigend bis 5 Liter/Sekunde und erreicht sein Maximum. Das Wasser läuft weitere 10 Sekunden mit maximaler Menge in die Wanne. Der Wasserhahn wird geschlossen und der Stöpsel gezogen. Das Wasser fließt mit 4 Liter/Sekunde konstant für 10 Sekunden ab. Wie viel Wasser befindet sich am Schluss in der Wanne?
Bevor man mit dem Rechnen anfängt, startet man eine Überlegung, wie das Ganze auszusehen hat. Es bietet sich an, das in einem Koordinatensystem zu veranschaulichen.
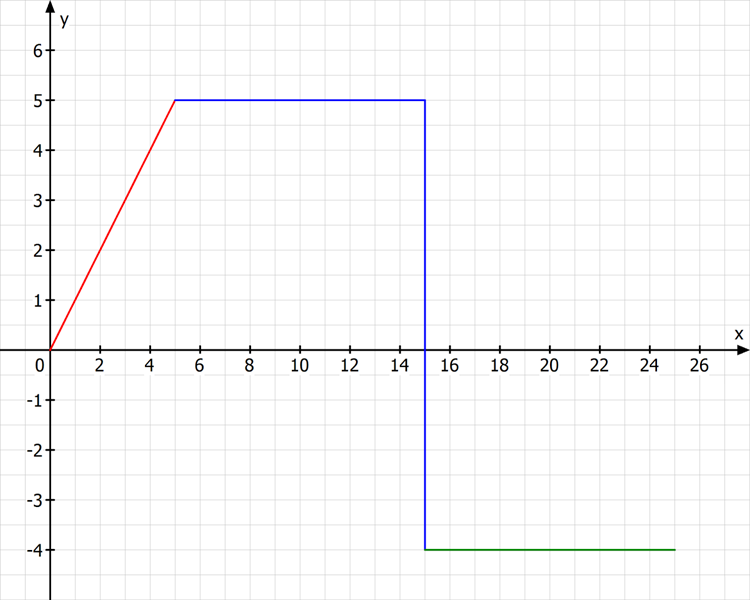
Die y-Achse ist hierbei die Anzahl der Liter und die x-Achse die Zeit in Sekunden. Es wird im roten Abschnitt der linear zunehmende Zufluss abgebildet. Im blauen Abschnitt der konstant gehaltene Zufluss vom Maximalwert (5 Liter/Sekunde) und im grünen Abschnitt der Abfluss von 4 Liter/Sekunde. Wenn wir die Gesamtfläche berechnen, erfahren wir, wie viel Wasser in der Wanne verblieben ist. Es ist dabei zu beachten, dass die grüne Fläche negativ zu interpretieren ist und von den anderen beiden abgezogen werden muss.
\( \int_0^5 x\; dx + \int_5^{15} 5\; dx - \int_{15}^{25} 4 \; dx \\ = \left[\frac12x^2\right]_0^5 + \left[5x\right]_5^{15} - \left[4x\right]_{15}^{25} \\ = \left(\frac12 · 5^2 - \frac12 · 0^2\right) +\left(5 · 15 - 5 · 5\right)-\left(4 · 25 - 4 · 15\right) \\ = 22,5 \)
Es ergibt sich eine Wassermenge von 22,5 Litern, die in der Wanne verbleiben.
Da die Funktionen hier sehr einfach gewählt sind, kann man dies auch ohne Integrale berechnen, indem man im obigen Schaubild die tatsächlichen Flächeninhalte berechnet. Für das rote Dreieck ergibt sich \( A = 5·5·\frac{1}{2} = 12,5 \), für das blaue Rechteck \( B = 10·5 = 50 \) und für das grüne Rechteck ergibt sich \( C = 4·10 = 40 \).
Verrechnet man diese Flächen ergibt sich \( A + B - C = 22,5 \). Genau das was wir über die Integrale berechnet hatten.
Ein Kanal hat einen parabelförmigen Querschnitt. Seine Scheiteltiefe beträgt 3,20 m, der Uferabstand ist mit 4,00 m angegeben. Die Wasserhöhe beträgt 75 % der Scheiteltiefe. Wie viel Wasser befindet sich in dem 500 m langen Kanal?
Um der Lösung näher zu kommen, bietet sich an, zuerst einen Graphen zu zeichnen. Dabei tragen wir den Kanal so ab, dass die Erdoberfläche der x-Achse entspricht und damit der Scheitel bei y = -3,2 liegt.
~plot~ 0.8x^2-3.2; -0,8 ~plot~ Der Wasserstand ist hier rot dargestellt und entspricht 75 % (also 3,2 · 0,75 = 2,4 → bei y = -0,8) vom Tiefpunkt aus.
Um die Fläche zwischen blau f(x) und rot g(x) zu bestimmen, stellen wir beide Funktionen auf und bilden die Differenzenfunktion.
\( f(x) = 0,8x^2 - 3,2 \\ g(x) = -0,8 \\ h(x) = f(x) - g(x) = 0,8x^2 - 2,4 \)
Die Nullstellen der Differenezenfunktion (Schnittstellen der Funktionen) sind:
\( h(x) = 0,8x^2-2,4 = 0 \\ 0,8x^2 = 2,4 \\ x^2 = 3 \\ x_{1,2} = \pm \sqrt{3} \)
Wir integrieren also nur bis zur \(\sqrt3\), nutzen dabei die Symmetrie und integrieren wie folgt:
\( 2 \left|\int_0^{\sqrt3} 0,8x^2 - 2,4 \; dx \right| \approx 5,54 \)
Dies ist die Querschnittsfläche des wassergefüllten Teils des Kanals.
Mit der Länge multipliziert ergibt sich das Volumen:
\(V = 500 \text{ m} · 5,54 \text{ m}^2 \approx 2~771 \text{ m}^3 \)
