Um die Fläche zwischen zwei Graphen zu bestimmen, gehen wir prinzipiell wie gewohnt vor. Der einzige größere Unterschied besteht in der Vorarbeit, bei der die Differenzfunktion der beiden Funktionen berechnet wird.
Dabei wird die Differenzfunktion im Betrag betrachtet (auch hier gilt wieder, dass meist erst der Wert des Integrals berechnet wird und erst davon der Betrag gezogen wird).
Beispiel
Nehmen wir die beiden Funktionen f(x) = x2 + 1 sowie g(x) = x + 1.
Die Differenzfunktion ist demnach h(x) = f(x) - g(x) (Wichtig: Es spielt keine Rolle, ob wir h(x) = f(x) - g(x) oder h(x) = g(x) - f(x) rechnen, da ja der Betrag verwendet wird).
Hat man die Differenzfunktion h(x) vorliegen, haben wir die ganze zusätzliche Vorarbeit erledigt und können vorgehen wie vorher gezeigt. Dazu werden die Nullstellen berechnet und in deren Grenzen integriert.
h(x) = x2+1 - (x+1)
= x2-x
= 0
x1 = 0 und x2 = 1
\( \left|\int \limits_0^1 h(x) \; dx \right| = \left|\int \limits_0^1 x^2-x \; dx\right| = \left|\left[\frac{1}{3} x^3-\frac12 x^2\right]_0^1\right| \)
\( = \left|\frac{1}{3} - \frac12 - (0)\right| = \left|-\frac{1}{6} \right| = \frac{1}{6} \)
Schauen wir uns das noch an ein paar Graphen an.
Zuerst betrachten wir die Fläche zwischen den beiden Graphen g und f der ursprünglichen Aufgabe:
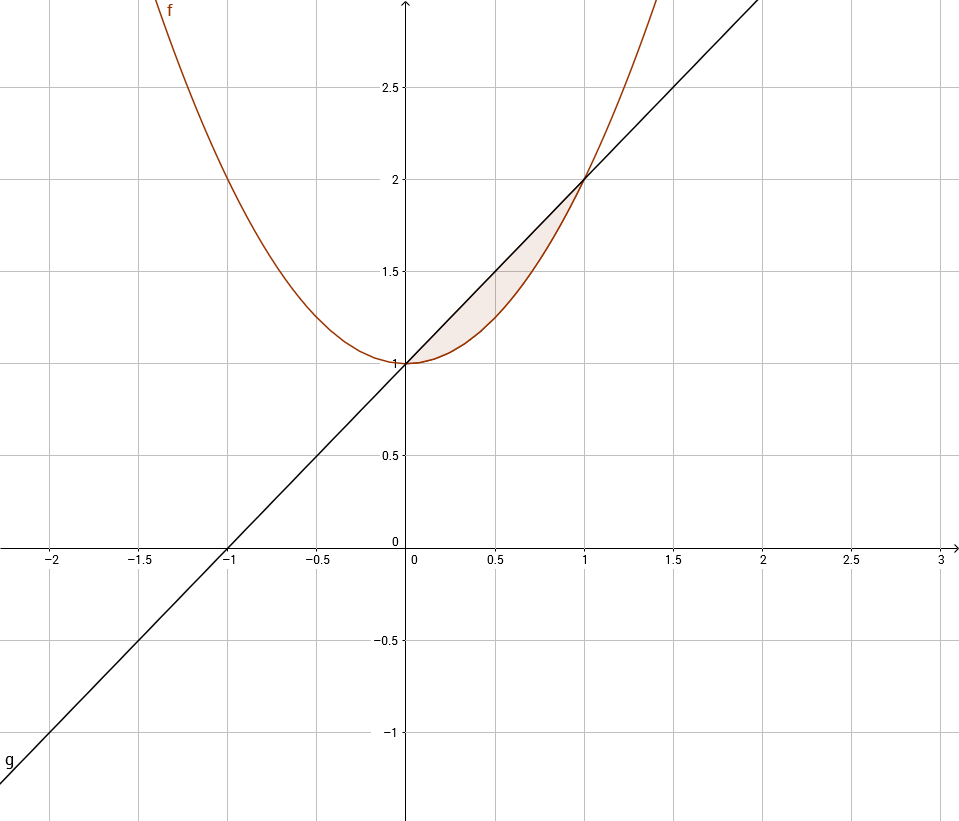
Hier erkennen wir auch die Schnittstellen zu x = 0 und x = 1, wie wir sie bestimmt haben. Errechnet wird der Flächeninhalt nun über die Differenzfunktion.
Die Differenzfunktion produziert nichts anderes als eine Vereinfachung, indem später nur noch die Fläche zwischen Graph und x-Achse berechnet werden muss. Was wir in Integralform hingeschrieben haben und so aussieht:
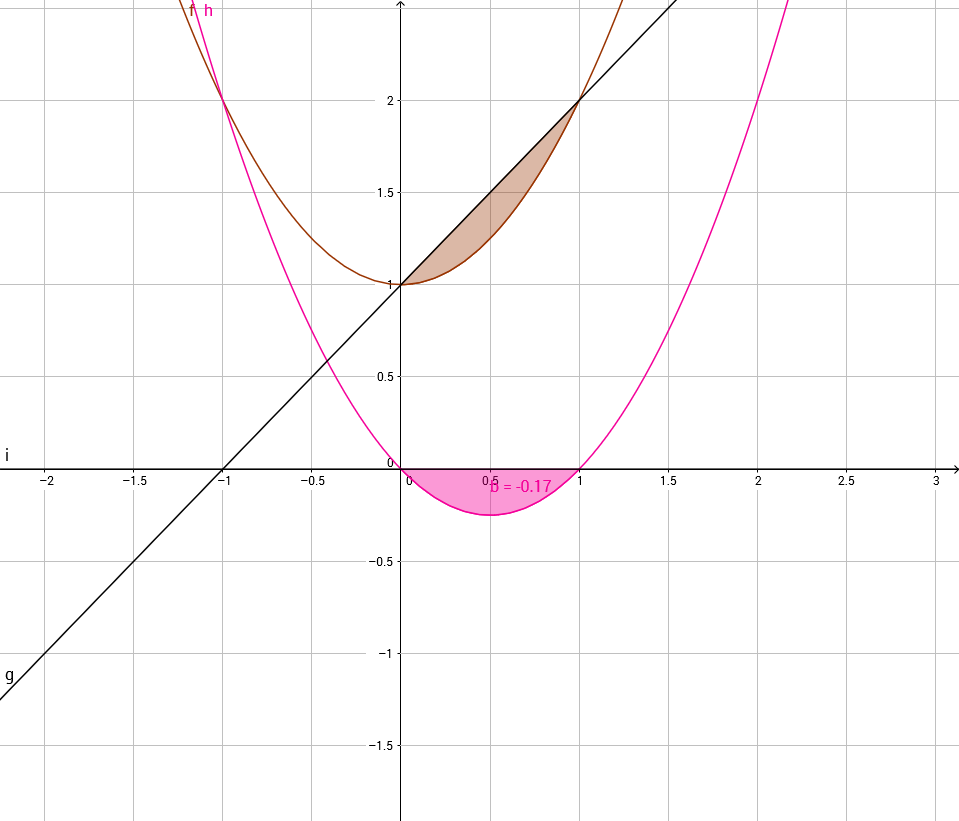
Das erinnert an die bisherigen Aufgaben und wir können dies nun wie gelernt lösen.
