Ein weiterer wichtiger Punkt soll noch erklärt werden, und zwar geht es um die Symmetrie bei Integralen (Vorsicht: Unabhängig von der Flächenberechnung).
Einen ersten Eindruck davon hatten wir schon in Beispiel 4 gewonnen. Dort hatten wir die Gesamtfläche berechnen sollen und erstmal ohne Betrag gerechnet. Das Ergebnis war 0. Dort waren wir aber an der Fläche interessiert und haben nachträglich noch die Beträge gesetzt. Halten wir uns das Beispiel nochmals vor Augen:
Punktsymmetrie
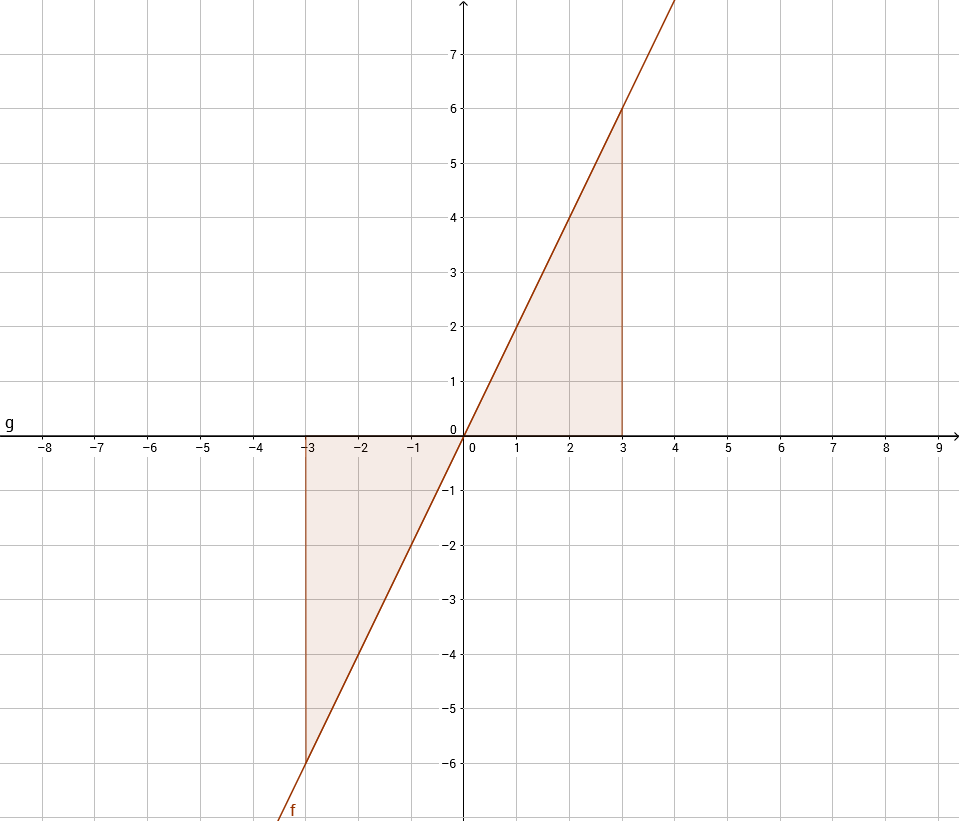
Es gilt sich zu merken, dass im Falle einer Berechnung von Integralen (unabhängig von der Flächenberechnung) die Punktsymmetrie bei der Bestimmung dieser helfen kann, da sich Integrale mitunter zu 0 aufheben.
\( \int \limits_{-3}^3 2x \; dx = \left[x^2\right]_{-3}^3 = 3^2 - (-3)^2 = 9-9 = 0 \)
So braucht man bei obigem Integral nur die Funktion f(x) = 2·x anzuschauen und sie als eine punktsymmetrische Funktion zu identifizieren; sowie die Grenzen, die sich je gleich weit vom Symmetriepunkt entfernt befinden, um direkt den Wert 0 ausgeben zu können.
Achsensymmetrie
Hier heben sich die Teilbereiche zwar nicht gegenseitig auf, doch kann man sich durchaus die Arbeit erleichtern, wenn man weiß, dass man nur die Hälfte eines Integrals zu berechnen hat und den errechneten Teil verdoppeln kann, um auf das Ergebnis zu kommen.
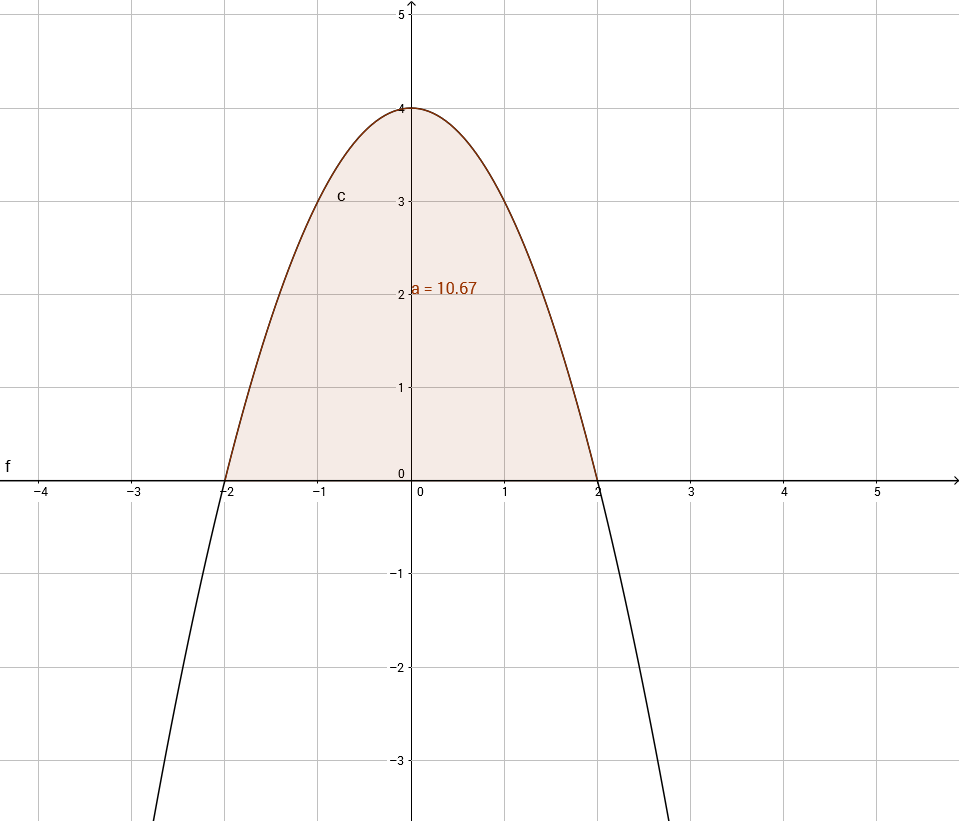
Um zur Funktion f(x) = -x²+4 den Flächeninhalt zu errechnen, hatten wir zuvor gerechnet:
\( \int \limits_{-2}^2 -(x-2)(x+2) \; dx= -\int \limits_{-2}^2 x^2-4 \; dx = -\left[\frac13x^3 - 4x\right]_{-2}^2 \\ = -\left(\frac13\cdot2^3 - 4\cdot2 - \left(\frac13 \cdot(-2)^3 - 4\cdot(-2)\right)\right) = -\left(-\frac{16}{3} - \frac{16}{3}\right) = \frac{32}{3} \)
Hingegen kann man auch nur von 0 bis 2 integrieren und diesen Flächeninhalt verdoppeln, um auf dasselbe zu kommen (oft ist es einfacher 0 als Grenze einzusetzen, als beispielsweise -2).
\( 2\int \limits_{0}^2 -(x-2)(x+2) \; dx= -2\int \limits_{0}^2 x^2-4 \; dx = -2\left[\frac13x^3 - 4x\right]_{0}^2 \)
\( = -2\left(\frac13\cdot2^3 - 4\cdot2 - 0\right) = -2\left(-\frac{16}{3} \right) = \frac{32}{3} \)
