AB: Lektion Quadratische Funktionen (Teil 8)
Nachfolgend findet ihr Aufgaben zu den quadratischen Funktionen, mit denen ihr euer neues Wissen testen könnt.
Bestimme die Funktionsgleichung einer verschobenen Normalparabel (also der Koeffizient vor dem x² ist 1), die den Scheitel S(2|3) hat. Gib die Funktionsgleichung in Scheitelpunktform und Allgemeinform an.
Bestimme die Funktionsgleichung einer verschobenen Normalparabel (also der Koeffizient vor dem x² ist 1), die den Scheitel S(2|3) hat. Gib die Funktionsgleichung in Scheitelpunktform und Allgemeinform an.
Die Scheitelpunktform kann direkt angegeben. Diese ist ja allgemein f(x) = a(x-d)² + e mit S(d|e). Bei uns ist dabei a = 1. Also:
f(x) = (x-2)² + 3
Die Allgemeinform erhalten wir, wenn wir ausmultiplizieren:
f(x) = (x-2)² + 3 | Binomische Formel anwenden
= x² - 4x + 4 + 3
= x² - 4x + 7
Eine Lumme (ein Vogel, der sich ins Wasser stürzt, um Fische zu fangen) beschreibt bei ihrem Tauchgang die Bahn einer Parabel mit der Funktionsgleichung f(x) = x² + 2·x - 15. Die Wasseroberfläche sei die x-Achse.
Zeichne die Parabel.
Für die Zeichnung eignet es sich wieder die Nullstellen zu berechnen um die Wertetabelle sinnvoll anlegen zu können:
x² + 2·x - 15 = 0 | p-q-Formel mit p = 2 und q = -15
x1 = -5 und x2 = 3
Eine sinnvolle Wertetabelle wäre dann beispielsweise:| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 0 | -7 | -12 | -15 | -16 | -15 | -12 | -7 | 0 |
Das ergibt dann den Graphen:
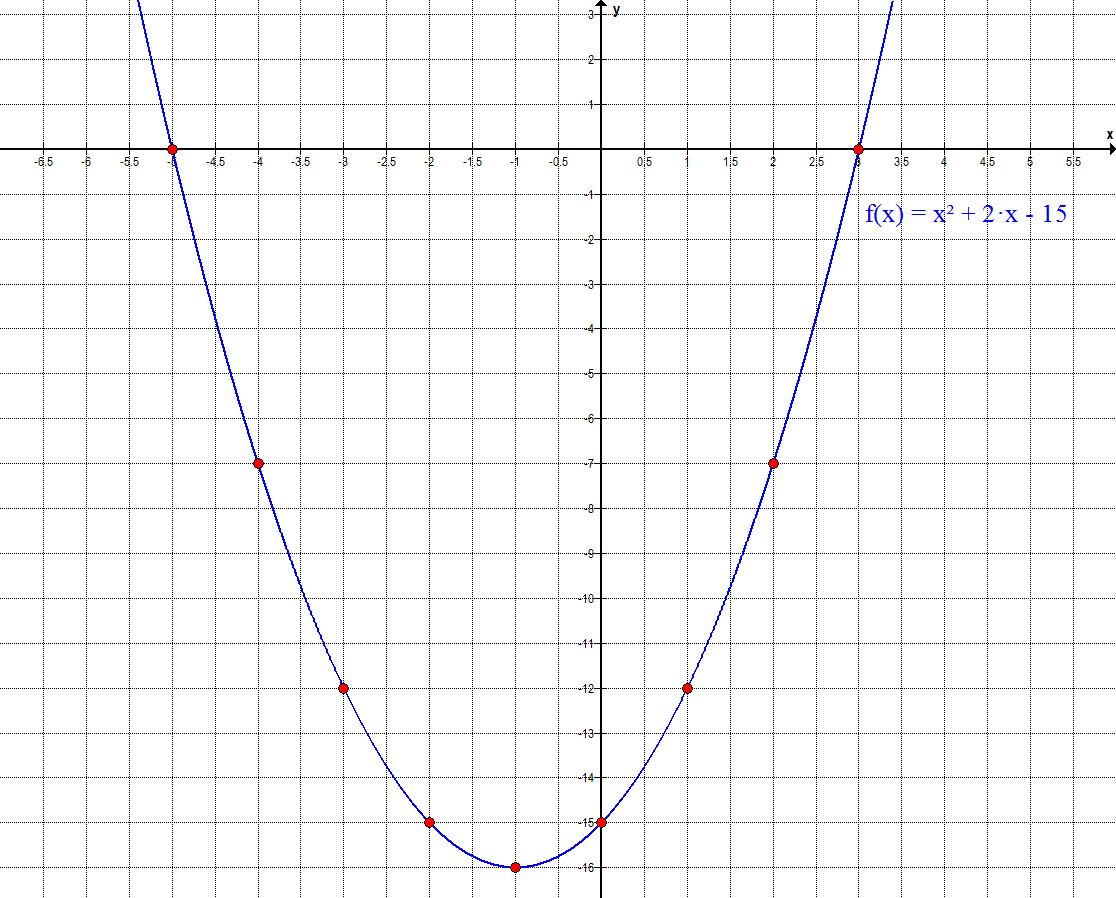
Wie viele Meter neben dem Eintauchpunkt taucht die Lumme wieder auf?
Die Lumme taucht bei den Nullpunkten ein und auf. Folglich braucht man nur die Differenz der Nullstellen zu bestimmen. Die Nullstellen haben wir schon bestimmt und deren Differenz ist d = 8. Die Lumme taucht also 8 m neben dem Eintauchpunkt wieder auf.
Wie tief taucht die Lumme?
Die Tiefe lässt sich wieder über den Scheitelpunkt bestimmen. Dies könnte man mit der Scheitelpunktform tun. Es gibt aber eine Alternative. Man muss dazu wissen, dass eine Parabel symmetrisch zu ihrem Scheitelpunkt ist. Das heißt, wenn man vom Scheitelpunkt aus eine bestimmte Strecke nach rechts geht und sich den y-Wert anschaut, ist derselbe y-Wert auch auf der linken Seite in gleicher Entfernung zu finden. Hat man in unserem Falle die Nullpunkte gegeben, also jeweils den y-Wert 0, dann weiß man, dass der Scheitelpunkt genau an der Stelle zwischen den beiden liegen muss. Dazu die Differenz der beiden Nullstellen bestimmten (d = 8) und durch 2 dividieren. Dies muss nun nur noch auf eine der Nullstellen addiert (bzw. subtrahiert) werden und man hat die Scheitelstelle:
Nullstelle war x = -5. Nun wird die halbe Differenz addiert:
+4 damit also: -5 + 4 = -1.
Bei x = -1 ist der Scheitelpunkt zu finden. Schaut man in der Wertetabelle nach, kann das wohl sein, denn hier ist auch der kleinste/tiefste Wert zu finden. Der Scheitelpunkt liegt bei S(-1|-16) und damit erreicht die Lumme eine Tiefe von 16 m.
