Geoknecht - Geometrische Körper in 3D erstellen

1. Farben: Den HEX-Farbcode am Ende der Zeile in Klammern setzen, Beispiel: kugel(3|3|1 2){F00}
2. Koordinatenebenen: Diese können mit Eingabe von koordinatenebenen(xy xz yz) eingeblendet werden, nicht benötigte weglassen. Ein # anfügen für Gitternetze.
3. Rotation: Quader, Würfel, Zylinder, Text können in x-y-z-Richtung rotiert werden, dazu die Winkel mit eckigen Klammern in Grad anfügen, Beispiel: würfel(2|2|3 4)[0|45|90]
4. Animation: Werte können schrittweise geändert werden, den Cursor auf die Zahl setzen, dann STRG ATL SHIFT halten und ↑ ↓ ← → drücken.
5. Kameraposition fixieren mit camera(x|y|z x|y|z), zuerst die Position der Kamera angeben, dann wohin geschaut wird. Wird der zweite Parameter weggelassen, dann wird der Koordinatenursprung (0|0|0) fokussiert.
6. Die Schriftgröße kann bei punkt und text skaliert werden, indem man z. B. %1.5% ans Ende der Textzeile setzt.
7. Um einen Kegel zu erstellen, wählt man sich einen zylinder(x|y|z h|r_D|r_G|s|o|α) und setzt r_G (Radius Grundfläche) auf den Wert 0. Zum Beispiel: zylinder(2|2|0 2|0|4|200)
8. Um eine Halbkugel oder Kugelteile zu erzeugen, nutzt man die erweiterte Syntax für die Kugel mit: kugel(x|y|z Radius, phiStart, phiLänge, thetaStart, thetaLänge) Dabei ist phiStart der horizontale Startwinkel, phiLänge ist der horizontale Krümmungswinkel, thetaStart ist der vertikale Startwinkel und thetaLänge ist der vertikale Krümmungswinkel. Hier ein Beispiel einer Halbkugel (Hemisphäre): kugel(0|0|4 4 0 6.28 1.55 3.14)
9. Hier ist ein Video, das den Geoknecht 3D vorstellt und seine Features zeigt: Geoknecht 3D - Stereometrie-Programm
10. Du hast noch einen Hinweis, was noch unklar ist? Schreib uns!

Die 3D-Navigation erfolgt mit der Maus:
· Linke Maustaste gedrückt halten, Maus bewegen, damit rotiert man die Kamera.
· Rechte Maustaste gedrückt halten, Maus bewegen, damit verschiebt man die Kamera im Raum.
· Mausrad drehen, damit zoomt man herein und heraus.

Man kann in der Eingabe beliebig viele Variablen festlegen (eine Variable pro Zeile). Hier ein paar Beispiele:
· $x=4 bei Quader, Vektor, Dreieck, Würfel
· $x=1|2|3 für Vektor mit Beschriftung
· $y=2 und $x=1|2|3 bei Vektor und Kugel
· $x=Test für mehrfache Textverwendung

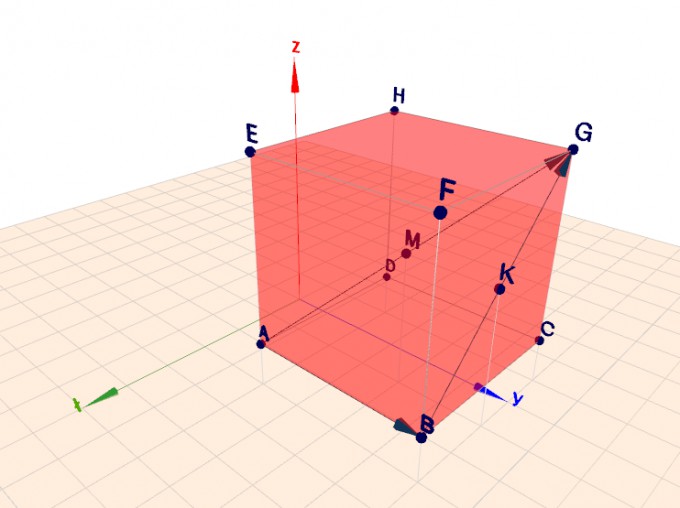• 3D-Koordinaten vom Würfel mit Raumdiagonale und Flächendiagonale
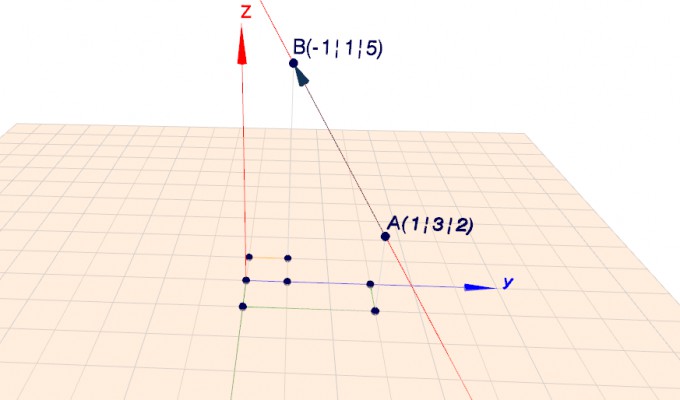• Gerade mit Hilfe von Stütz- und Richtungsvektor skizzieren
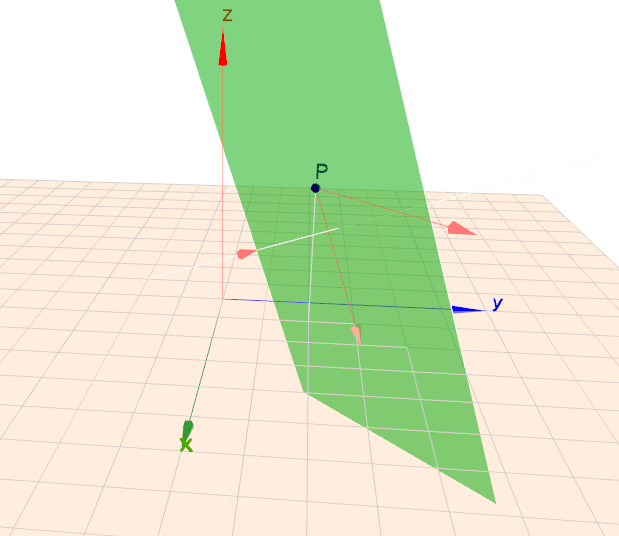• Ebene im Raum
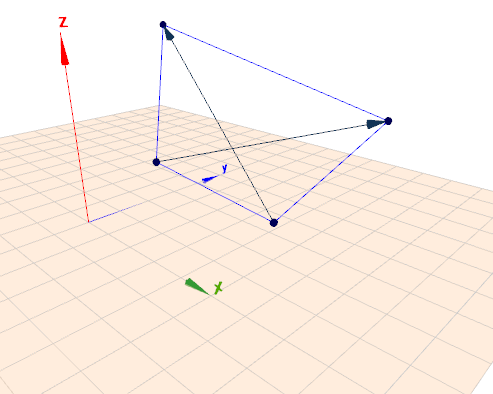• Vektoren und ebenes Viereck
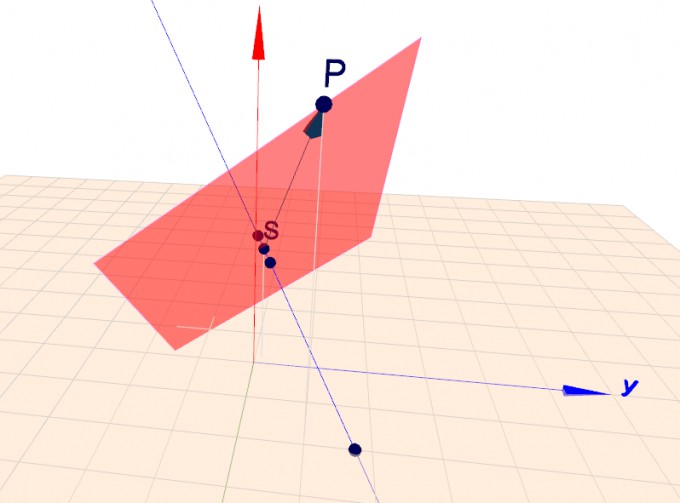• Ebene, Vektor und Gerade und ihr Schnittpunkt
• Geraden mit Spurpunkten
• Koordinatenebenen
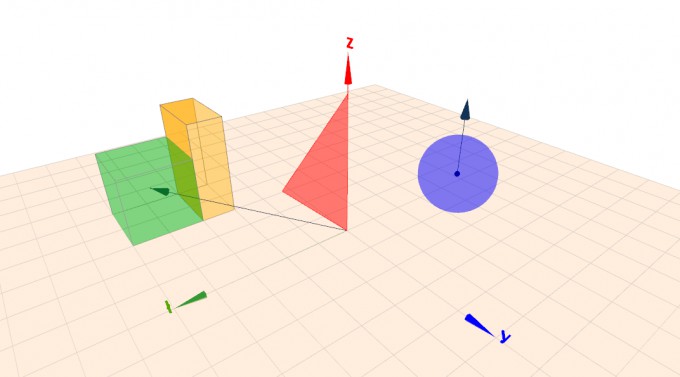• Beispiele für Kugel, Quader, Würfel, Dreieck, Vektor
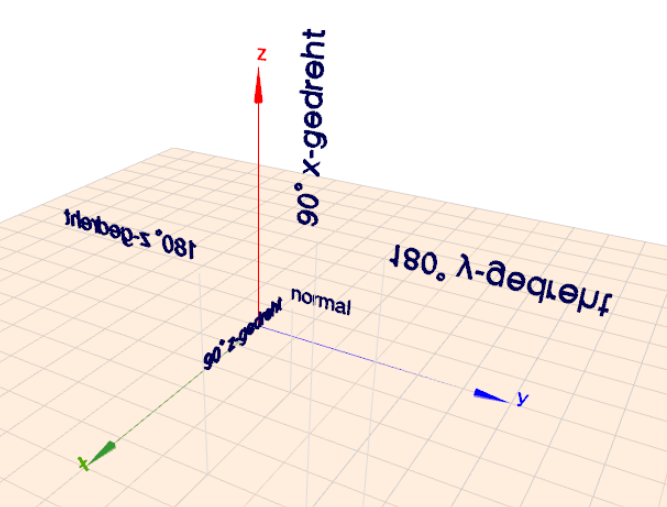• Beispiele für Text-Rotation
• Beispiele für Quader-Rotationen
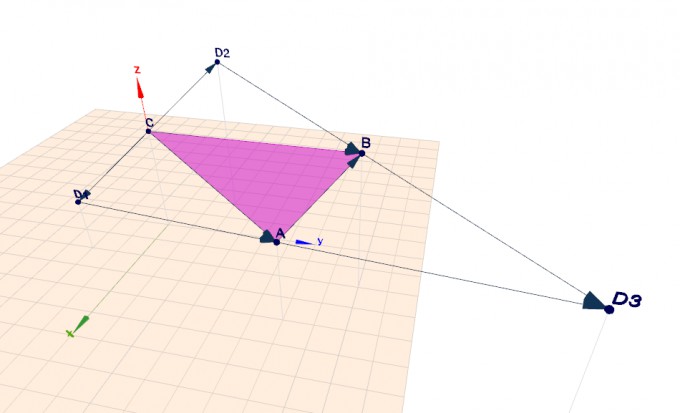• Dreieck zu einem Parallelogramm ergänzen (mit Hilfe von Vektoren)
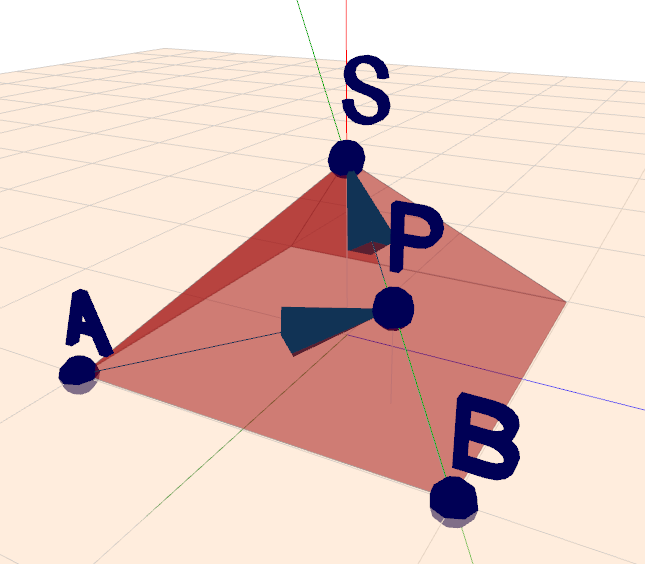• Gelaufener Weg auf einer Pyramide
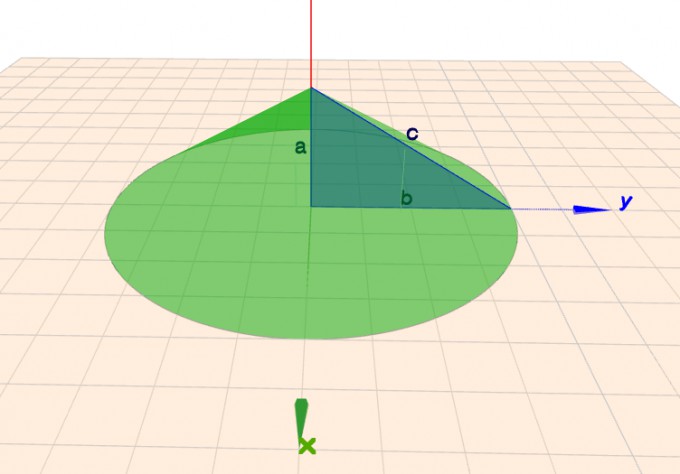• Kegel mit einbeschriebenem rechtwinkligen Dreieck
• Halbkugel
• 
• 
• 

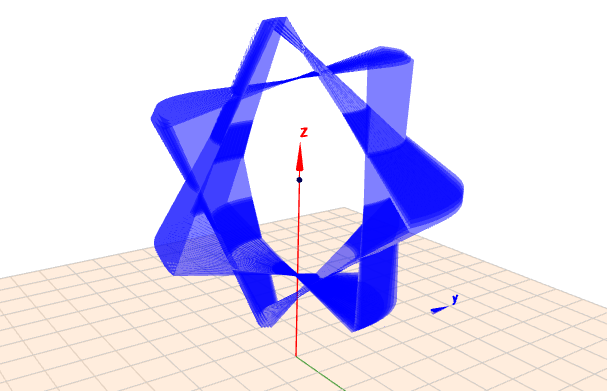
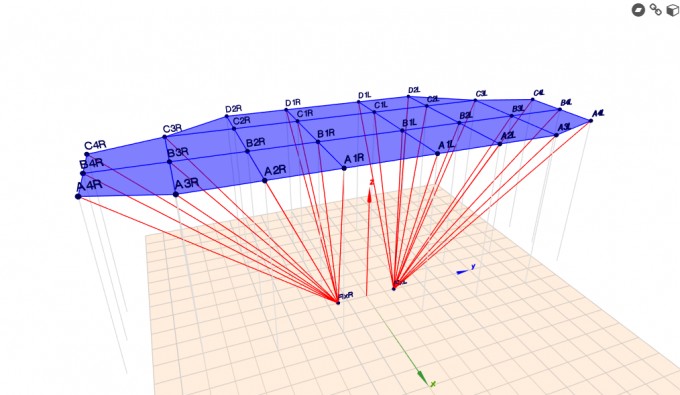
Du hast eine interessante 3D-Grafik erstellt, dann schick uns den Geoknecht-Code an .

Eingegangene Zusendungen:

• Simon Zhong

If you need this program in English, look here: Geoservant 3D