CHECK: Quadratische Funktionen I
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
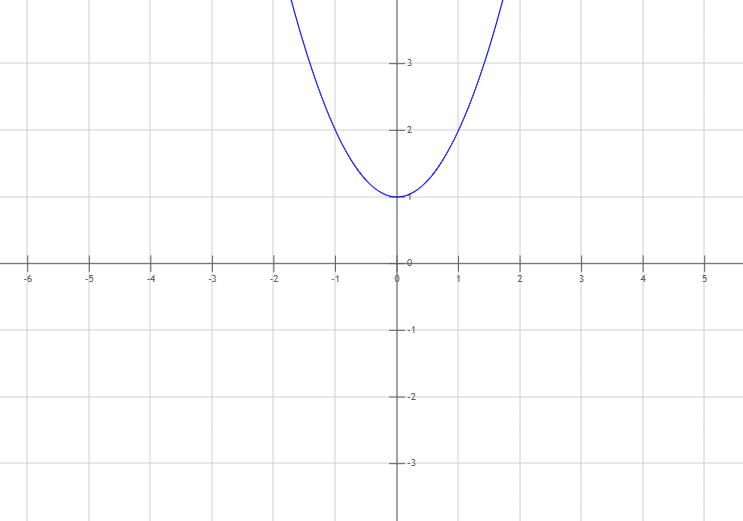
Welche der Abbildungen entspricht der Funktion f(x) = (x+2)²?
Bei f(x) = (x+2)² erkennen wir an der +2 innerhalb der Klammer, dass der Scheitelpunkt der Parabel 2 nach links verschoben wird zur Stelle -2. Bzw. setzen wir x = -2 in die Funktionsgleichung, so ergibt sich: f(-2) = (-2+2)² = 0² = 0, also der Punkt Sx(-2 | 0).
Zusätzlich sehen wir anhand der Grafik, dass ein Achsenschnittpunkt Sy(0 | 4) ist. Damit muss (wenn wir x = 0 einsetzen) f(0) = 4 sein. Dies ist bei f(x) = (x+2)² der Fall mit f(0) = (0+2)² = 2² = 4.
Wie lautet die Allgemeinform der Scheitelpunktform f(x) = 3·(x+2)²?
Gleichung mit erster binomischer Formel ausrechnen:
f(x) = 3·(x+2)²
f(x) = 3·(x²+2·x·2 + 2²)
f(x) = 3·x²+3·2·x·2 + 3·2²
f(x) = 3·x²+12·x + 3·4
f(x) = 3·x²+12·x + 12
Der Turmspringer und der Sprungturm
Die Flugbahn eines Turmspringers kann man mit h(l) = -10 l² + n beschreiben, wobei h die Höhe, l der horizontale Abstand zum Sprungturm und n die Höhe des Sprungturmes beschreiben. Der Springer kommt nun 0,5 m vom Turm entfernt auf dem Boden auf. Bestimme die Höhe des Turms.
Beim Aufprall gilt: g(l) = 0.
Außerdem lässt sich sagen, dass l = 0,5 m ist.
Somit ergibt sich:
0 = -10 · 0,5² + n
10 · 0,5² = n
n = 10 · \( \frac{1}{4} \) = \( \frac{10}{4} \) = 2,5
Funktionsgraph:
~plot~ -10x^2+2,5;hide ~plot~
Was ist der Unterschied zwischen quadratischer Gleichung und quadratischer Funktion?
Eine quadratische Gleichung wird in folgender Form (Allgemeinform) notiert:
a·x² + b·x + c = 0
Wobei a, b und c für beliebige Zahlen stehen.
Eine quadratische Funktion notieren wir hingegen in der Form:
f(x) = a·x² + b·x + c = y
Wie wir bei den quadratischen Funktionen gelernt haben, beschreibt die quadratische Funktion einen Graphen im Koordinatensystem. Die quadratische Gleichung hingegen setzt die Funktionsgleichung null, sodass wir deren Nullstellen berechnen können.
Anders ausgedrückt:
Für die Funktion können wir unendlich viele x-Werte einsetzen und erhalten jeweils einen y-Wert als Lösung. Bei der quadratischen Gleichung erhalten wir zwei Werte, einen Wert oder keinen Wert für x als Lösung. Wir suchen bei der Gleichung also nach den x-Werten, für die die vorliegende Gleichung erfüllt ist ("Lösungsmenge").
Als quadratische Gleichung können wir also jede Gleichung bezeichnen, bei der ein x² als höchste Potenz vorkommt. Zum Beispiel: 3x + 2 = x². Diese Gleichung könnten wir jetzt umformen zu 0 = x² - 3x - 2 und von dieser Form (Normalform) ausgehend die p-q-Formel anwenden, um die beiden Lösungen für x auszurechnen. Das entspricht dem Sachverhalt, dass wir für eine Funktion f(x) = x² - 3x - 2 die Nullstellen ermitteln.
Fortschritt: