Beim Distributivgesetz wird eine Zahl (erster Faktor) mit einem Klammerterm (zweiter Faktor) multipliziert, der aus mindestens zwei Summanden besteht. Beispiel: 4·(5 + 3). Dadurch löst sich die Klammer auf und der Faktor wird zu jedem Summanden innerhalb der Klammer multipliziert.
Beispiel: 4·(5 + 3) = 4·5 + 4·3
Wir sagen hierzu auch „Ausmultiplizieren“.
Im Beispiel oben wird die 4 auf die 5 und 3 verteilt. Auf Lateinisch heißt „verteilen“ „distribuere“, daher sprechen wir vom Distributivgesetz (Verteilungsgesetz).
Allgemein: a·(b + c) = a·b + a·c
Die Animation zeigt, wie allgemeine eine Zahl a auf b und auf c verteilt wird:
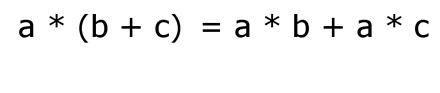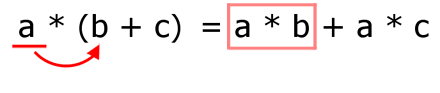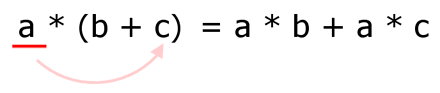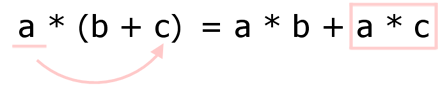
Nachstehend ist das Distributivgesetz mit Variablen und Zahlen dargestellt:
a·(b + c) = a·b + a·c
3·(4 + 1) = 3·4 + 3·1
3·5 = 12 + 3
15 = 15
Bitte merkt euch, dass das Distributivgesetz auch gilt, wenn die Zahl (der Faktor) hinter der Klammer steht. Zum Beispiel:
3·(12+18) = (12+18)·3 = 3·12 + 3·18
Verstecken wir eine Zahl, indem wir sie mit einer Variablen ersetzen, dann erhalten wir:
3·(x+18) = (x+18)·3 = 3·x + 3·18
Da die Division die Umkehrung der Multiplikation ist, können wir auch hier das Distributivgesetz anwenden:
(30+60):3 = 30:3 + 60:3
Führen wir das Distributivgesetz „rückwärts“ aus, dann sprechen wir vom Ausklammern.

