Eine Summe einer Summe wird Doppelsumme genannt. Was das bedeutet, macht ein Beispiel deutlich:
\( \sum \limits_{n=1}^{3} \sum \limits_{k=1}^{2}{n·k^2} \)
Wir benutzen die Bezeichnungen „Äußere Summe“ und „Innere Summe“ wie nachstehend gut zu erkennen ist:
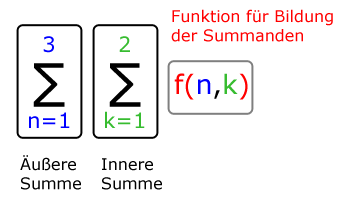
Wir legen für n den Startwert fest und laufen dann k ab. Anschließend wählen wir das nächste n und laufen k wieder ab. Und so weiter. Tun wir das für unser n·k2:
\( \sum \limits_{\textcolor{blue}{n=1}}^{\textcolor{blue}{3}} \sum \limits_{\textcolor{green}{k=1}}^{\textcolor{green}{2}}{\textcolor{blue}{n}·\textcolor{green}{k}^2} \)
∑∑ mit n = 1 → 1·12 + 1·22
∑∑ mit n = 2 → 1·12 + 1·22
+
2·12 + 2·22
∑∑ mit n = 3 → 1·12 + 1·22
+
2·12 + 2·22
+
3·12 + 3·22
\( \sum \limits_{\textcolor{blue}{n=1}}^{\textcolor{blue}{3}} \sum \limits_{\textcolor{green}{k=1}}^{\textcolor{green}{2}}{\textcolor{blue}{n}·\textcolor{green}{k}^2} = 30 \)

