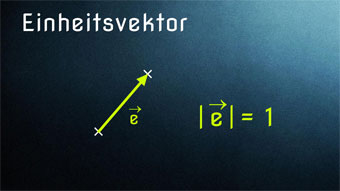
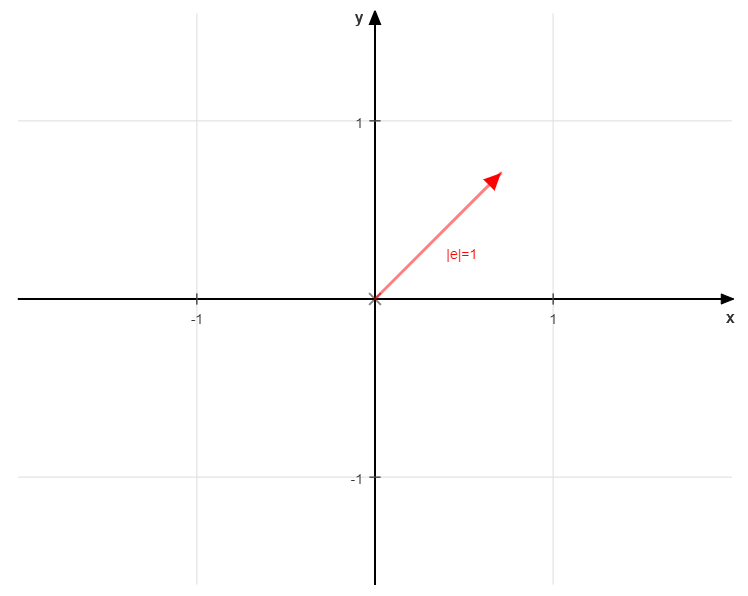
Ein Vektor mit der einheitlichen Länge 1 wird „Einheitsvektor“ genannt. Wir schreiben für Einheitsvektor meist \( \vec{e} \). Damit lässt sich der Einheitsvektor definieren als: \( |\vec{e}| = 1 \)
Wir können zu jedem Vektor (außer dem Nullvektor mit der Länge 0) einen dazugehörigen Einheitsvektor berechnen.
Dabei zeigt der gebildete Einheitsvektor in die gleiche Richtung wie der Vektor. Um die Dazugehörigkeit zu kennzeichnen, setzt man den Vektornamen in den Index des Einheitsvektors:
Ursprünglicher Vektor ist \( \vec{a} \), sein Einheitsvektor \( \vec{e_{a}} \).
Wenn man den Einheitsvektor mit dem Betrag des ursprünglichen Vektors multipliziert, kommt man wieder auf diesen Vektor.
Berechnung des Einheitsvektors
Ziel ist es, den gegebenen Vektor zu „normieren“, also auf die Länge 1 zu bringen.
Hierfür dividieren wir den Vektor (nennen wir ihn \( \vec{a} \)) durch seine Länge. Allgemein notiert:
$$ \vec{e_{a}} = \frac{\vec{a}}{|\vec{a}|} $$
Beispiel zur Berechnung:
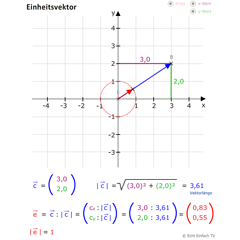
Gegeben sei der Vektor \( \vec{a} = \begin{pmatrix} 4\\3 \end{pmatrix} \). Für diesen soll nun der Einheitsvektor bestimmt werden.
Die Formel zur Berechnung des Einheitsvektors lautet:
\( \vec{e_{a}} = \frac{\vec{a}}{|\vec{a}|} \)
Zuerst müssen wir die Vektorlänge \( |\vec{a}| \) bestimmen. Diese berechnet sich mittels Satz des Pythagoras:
$$ |\vec{a}| = \sqrt{4^2 + 3^2} = \sqrt{25} = \textcolor{#00F}{5} $$
Nun können wir die Werte in unsere Formel einsetzen:
$$ \vec{e_{a}} = \frac{\vec{a}}{|\vec{a}|} \\ \vec{e_{a}} = \frac{ \begin{pmatrix} 4\\3 \end{pmatrix} }{ \textcolor{#00F}{5} } = \begin{pmatrix} \frac{4}{5} \\ \frac{3}{5} \end{pmatrix} = \begin{pmatrix} 0,8 \\ 0,6 \end{pmatrix} $$
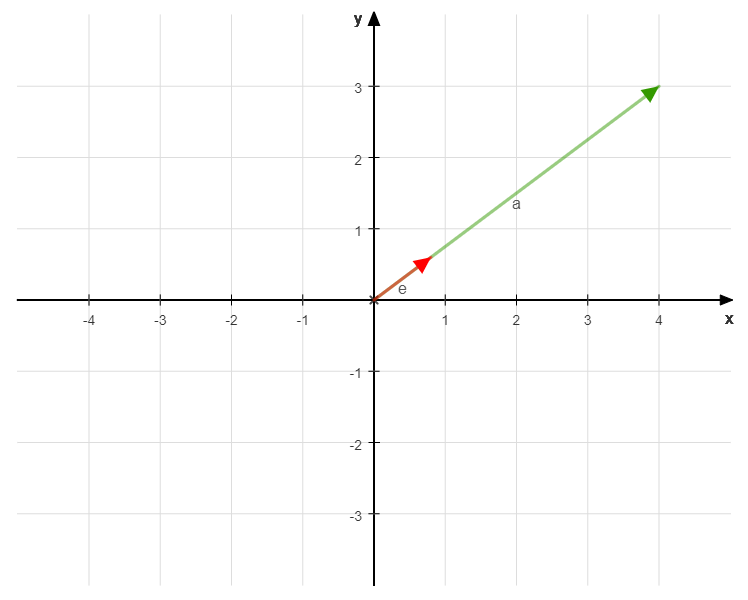
Zeichnen wir den Vektor und seinen Einheitsvektor:
Wir erkennen, dass beide in die gleiche Richtung zeigen.
Merken wir uns also die:
Allgemeine Formel zur Berechnung des Einheitsvektors (mit Komponenten x und y):
\( \vec{e_{a}} = \frac{\vec{a}}{|\vec{a}|} = \frac{ \begin{pmatrix} \frac{x}{y} \end{pmatrix} }{ |\vec{a}| } = \begin{pmatrix} \frac{x}{|\vec{a}|} \\ \frac{y}{|\vec{a}|} \end{pmatrix} \)
Länge des Einheitsvektors
Berechnen wir die Länge des Einheitsvektors aus obigem Beispiel, um zu prüfen, ob seine Länge auch wirklich 1 ist:
$$ |\vec{e}| = \sqrt{0,8^2 + 0,6^2} = \sqrt{0,64 + 0,36} = \sqrt{1} = 1 $$
Korrekt. Die Länge des Einheitsvektors ist 1.