Die Basisvektoren gibt es übrigens nicht nur im Zweidimensionalen (Ebene), sondern auch im Dreidimensionalen (Raum). Die Basisvektoren notiert man dort wie folgt:
$$ \vec{e_x} = \begin{pmatrix} 1\\0\\0 \end{pmatrix} \quad \vec{e_y} = \begin{pmatrix} 0\\1\\0 \end{pmatrix} \quad \vec{e_z} = \begin{pmatrix} 0\\0\\1 \end{pmatrix}$$
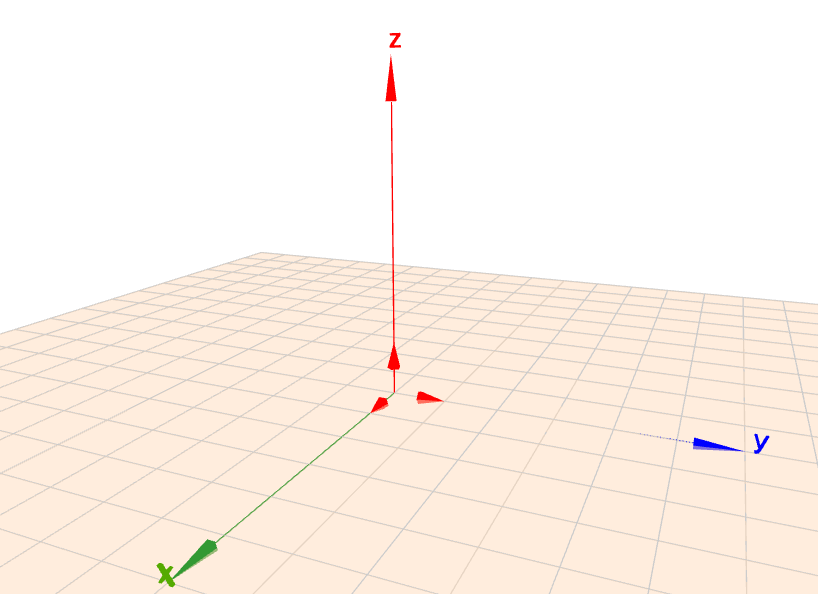
Grafisch kann man sie in den Ursprung des Koordinatensystems zeichnen. Die Basisvektoren (in folgender Abbildung rot dargestellt) liegen auf den Achsen und haben die Länge 1.
Mit diesen drei Basisvektoren und der Skalarmultiplikation können wir nun jeden beliebigen Vektor im Raum bilden. Man nennt sie auch „Standard-Basisvektoren“ des dreidimensionalen Vektorraums ℝ3.