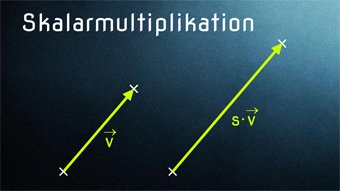
Bei der Skalarmultiplikation multiplizieren wir einen festen Wert mit allen Komponenten eines Vektors.
\( s·\vec{v} = \vec{r} \)
Dadurch verkürzt oder verlängert sich der Vektor entsprechend:
- s = 1 keine Skalierung
- s > 1 Vektorstreckung
- 0 < s < 1 Vektorstauchung
- s = 0 Nullvektor
- -1 < s < 0 gestauchter Gegenvektor
- s = -1 Gegenvektor
- s < -1 gestreckter Gegenvektor
Wenn der Skalar positiv ist, bleibt die Vektorrichtung unverändert.
Ist der Skalar negativ, kehrt sich die Vektorrichtung um, der Vektor zeigt dann in die entgegengesetzte Richtung.