Sofern wir die Höhe eines Dreiecks ermitteln wollen, stehen uns zwei Formeln zur Verfügung.
Wir können die Höhe bereits berechnen, wenn uns die Dreiecksseiten a, b und c gegeben sind (mit Hilfe des Kosinussatzes).
Genauso können wir die Höhe berechnen, wenn wir die Teilstrecken p und q kennen. Dazu benutzen wir den sogenannten Höhensatz des Euklid, der aus zwei Höhenformeln für das rechtwinklige Dreieck besteht:
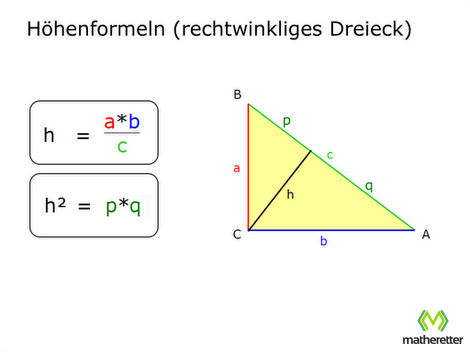
Die Formel h² = q·p bezeichnet man auch als Höhensatz des Euklid. Die Herleitung sei im Folgenden aufgeführt. Die Unbekannten sind gemäß Dreiecksgrafik oben benannt:
p² = a² - h²
→ a² = p² + h²
q² = b² - h²
→ b² = q² + h²
Mit Satz des Pythagoras:
a² + b² = c² | Einsetzen der Formeln für a² und b²
(p² + h²) + (q² + h²) = c²
p² + h² + q² + h² = c²
p² + q² + 2·h² = c² | c ergibt sich aus (p+q)
p² + q² + 2·h² = (p+q)²
p² + q² + 2·h² = p² + 2·p·q + q²
p² + q² + 2·h² = p² + 2·p·q + q² | -q² - p²
2·h² = 2·p·q | :2
h² = p·q