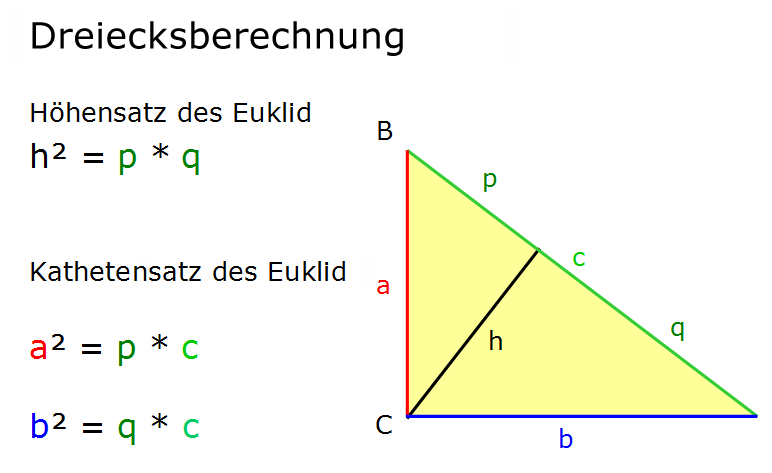
Erinnern wir uns, die Katheten sind die beiden kurzen Seiten des Dreiecks, also Seiten a und b. Wenn wir die Höhe auf c einzeichnen, erhalten wir die folgende bereits bekannte Grafik:
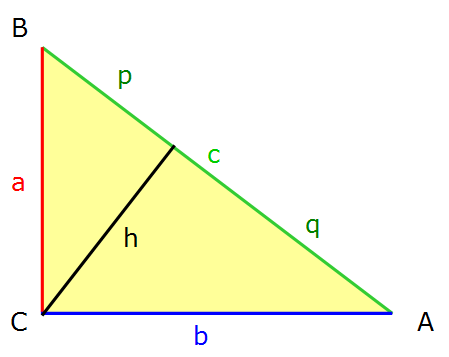
Es sind zwei kleine rechtwinklige Dreiecke entstanden, auf die wir nun den Satz des Pythagoras anwenden könnnen:
a² = p² + h² | für h² setzen wir den Höhensatz von oben ein mit h²=p·q
a² = p² + (p·q) | p ausklammern
a² = p · (p + q) | (p+q) ist ja c, also ersetzen wir den Term mit c
a² = p · c | das ist der 1. Teil des Kathetensatzes
Nun betrachten wir das zweite kleine Dreieck:
b² = q² + h² | für h² setzen wir den Höhensatz von oben ein mit h²=p·q
b² = q² + (p·q) | q ausklammern
b² = q · (q + p) | (q+p) ist ja c, also ersetzen wir den Term mit c
b² = q · c | das ist der 2. Teil des Kathetensatzes
Höhensatz und Kathetensatz des Euklid (Grafik)
Nachstehend eine Grafik, die den Höhensatz und Kathetensatz des Euklid darstellt: