Ein gerader Kegel* ist ein geometrischer Körper. Er besteht aus einer Kreisfläche am Boden (Grundfläche) und einer umlaufenden Mantelfläche, die in einem spitzen Winkel auf der Grundfläche steht und sich in einem Punkt oben schließt (Spitze des Kegels).
*Es gibt auch schiefe Kegel.
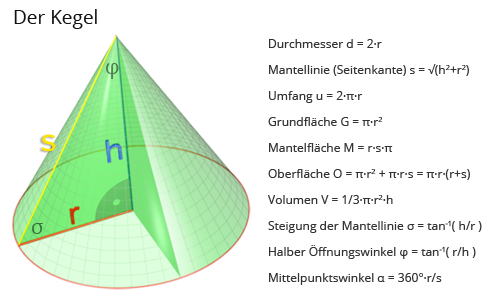
Link zur Grafik: https://www.matheretter.de/img/wiki/kegel-formeln.png
Kreisflächen sind für diesen Körper von wesentlicher Bedeutung, daher benötigt man die Formeln für den Kreis.
Merkmale
- Der Kegel hat 2 Flächen (Grund- und Mantelfläche), eine Ecke (die Spitze) und eine Seite (Kante, also die Kreislinie).
- Er ist achsensymmetrisch zur Kegelhöhe, also der Senkrechten, die durch die Spitze und den Mittelpunkt der Grundfläche verläuft.
- Radius und Durchmesser des Kegels sind an der kreisförmigen Grundfläche zu messen.
- Die Kreislinie der Grundfläche wird auch "Leitkurve" genannt.
- Die Mantellinien sind alle Linien, die sich auf der Mantelfläche befinden und von der Leitkurve direkt zur Kegelspitze führen.
- Die direkte Strecke von der Spitze zum Mittelpunkt der Grundfläche ist die Höhe des Kegels. Die Höhe steht stets senkrecht auf der Grundfläche.
- Kegelvolumen ist der Rauminhalt, der durch die Kegeloberfläche begrenzt wird.
- Die Kegeloberfläche ergibt sich aus Addition der Mantelfläche und der Grundfläche.
Beispiele aus dem Alltag (Kegelform)
Mütze, Zuckertüte (Einschultüte), Eiswaffel, Straßenhut, Turmdach, Sektglas, Speerspitze etc.
