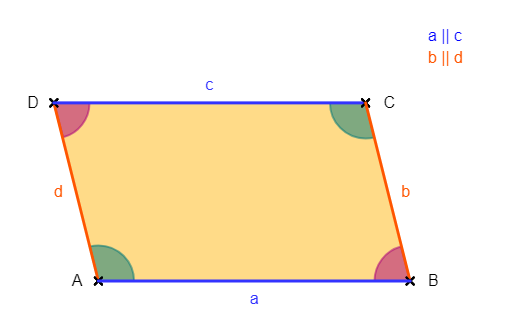
Ein Parallelogramm (auch „Rhomboid“ genannt) ist ein Viereck, eine geometrische Figur, die aus 4 Seiten besteht. Dabei sind die 2 jeweils gegenüberliegenden Seiten gleich lang und parallel zueinander. Aneinanderliegende Seiten bilden jeweils Winkel, die Größen zwischen 0° und 180° annehmen können. Die Summe aller Innenwinkel beträgt 360°.
Ein Parallelogramm ist ein Viereck, bei dem die gegenüberliegenden Seiten gleich lang und parallel zueinander sind. Zwei Winkel sind jeweils gleich groß.
Merkmale des Parallelogramms
- Das Parallelogramm hat 4 Ecken, 4 Seiten und 1 Fläche.
- Alle Innenwinkel sind zwischen 0° und 180° groß.
- Die gegenüberliegenden Winkel sind gleich groß.
- Das Parallelogramm ist punktsymmetrisch zu seinem Ursprung.
- Die Flächendiagonalen haben unterschiedliche Längen, sofern alle Winkel ungleich 90° sind.
- Die Flächendiagonalen schneiden sich in einem Punkt, der beide Diagonalen halbiert.
- Betrachtet man den Schnittpunkt der beiden Flächendiagonalen und alle Punkte des Parallelogramms, so erkennt man jeweils 2 zueinander kongruente (deckungsgleiche) Dreiecke.
- Ein Parallelogramm gehört zur Gruppe der Polygone (Vielecke).
- Stehen beim Parallelogramm alle Seiten im rechten Winkel zueinander (bzw. sind alle Innenwinkel rechte Winkel), so spricht man von einem Rechteck. Sind zusätzlich noch alle Seiten gleich lang, so spricht man von einem Quadrat.
- Sind beim Parallelogramm alle Seiten gleich lang und die Innenwinkel keine rechten Winkel, so spricht man von einer Raute (Rhombus).
- Die Parallelogrammgleichung lautet e2+f2 = 2·(a2+b2).
- Es gibt keinen Inkreis und keinen Umkreis.