Einführung Reelle Zahlen ℝ
Es mag erstaunlich sein, dass die Menge der Rationalen Zahlen, obwohl beliebig viele feingestufte Rationale Zahlen generierbar sind, immer noch (unendlich viele) Lücken auf dem Zahlenstrahl verbleiben. Diese Lücken werden durch Zahlen gefüllt, die nicht durch Anwendung der Grundoperationen aus Ganzen Zahlen gewonnen werden können, die Reellen Zahlen.
Beispiele hierfür sind die meisten Wurzeln, die Eulersche Zahl e oder die Kreiszahl π. Weil diese Zahlen nicht als Brüche Ganzer Zahlen dargestellt werden können, werden sie auch irrational genannt. Aus dem gleichen Grund ist für die Darstellung solcher Zahlen der Dezimalbruch besser geeignet.
Gemäß ihrer Entstehung werden die Reellen Zahlen unterschieden in Algebraisch und in Transzendent Irrationale Zahlen.
Algebraisch Irrationale Zahlen
Diese Menge von Zahlen ist Ergebnis algebraischer Operationen, wie z.B. Wurzelberechnungen, die Nullstellenermittlung von Polynomen oder anderer beliebiger mathematischer Ausdrücke.
Schon in der Antike wurde die Frage nach der Konstruierbarkeit von geometrischen Figuren wie Rechtecken oder Kreisen diskutiert. Unter anderem wurde dabei die Frage aufgeworfen, ob denn nicht die Quadratwurzel aus beliebigen Zahlen (Lösung des Satzes des Pythagoras) durch Verhältnisse von Ganzen Zahlen dargestellt werden kann.
Die Antwort auf diese Frage kann durch einen indirekten Beweis erbracht werden:
Beispiel:
Es ist zu beweisen, dass die Quadratwurzel aus 2 nicht durch eine Rationale Zahl darstellbar ist.
Voraussetzung: p, q seien teilerfremde Natürliche Zahlen
Behauptung: \( \sqrt{2} = \frac{p}{q} \quad \Rightarrow \quad 2 · {q^2} = {p^2} \)
Beweis:
Aus der Behauptung folgt, dass p² eine gerade Zahl sein muss.
Wenn aber p² gerade ist, muss auch p gerade sein (wurde bereits im Kapitel Indirekter Beweis bewiesen)
also:
\( p = 2 · p' \quad (\text{ p ist immer gerade! }) \quad \Rightarrow \quad 2 · {q^2} = 4 · {(p')^2} \)
\({q^2} = 2 · {(p')^2}\)
q² muss also auch gerade sein. Damit sind p und q nicht teilerfremd, da ja durch zwei teilbar. Das steht in einem Widerspruch zur Voraussetzung.
Folglich kann die Quadratwurzel aus 2 nicht durch Rationale Zahlen abgebildet werden.
q.e.d
Transzendent Irrationale Zahlen
Solche Zahlen wie e oder π hingegen werden transzendent irrational genannt. Sie können zwar auch z.B. durch eine → Reihenentwicklung annähernd berechnet werden, können aber nie mit letzter Genauigkeit bestimmt werden. Diese Zahlen haben aber eine zweckgebundene Bedeutung. Es ist deshalb weniger wichtig, wie genau diese Zahlen bekannt sind, sondern vielmehr ihre fundamentale Bedeutung bei der Lösung mathematischer Probleme.
Mächtigkeit von Reellen Zahlen
Infolge der Tatsache, dass kein Bildungsgesetz für Reelle Zahlen, wie es das etwa für die Rationalen Zahlen gibt, existiert, ist diese Menge nicht mehr abzählbar, sie ist überabzählbar unendlich und damit nicht mehr gleichmächtig zu den vorgenannten Zahlenmengen!
Zahlenstrahl und Intervalle
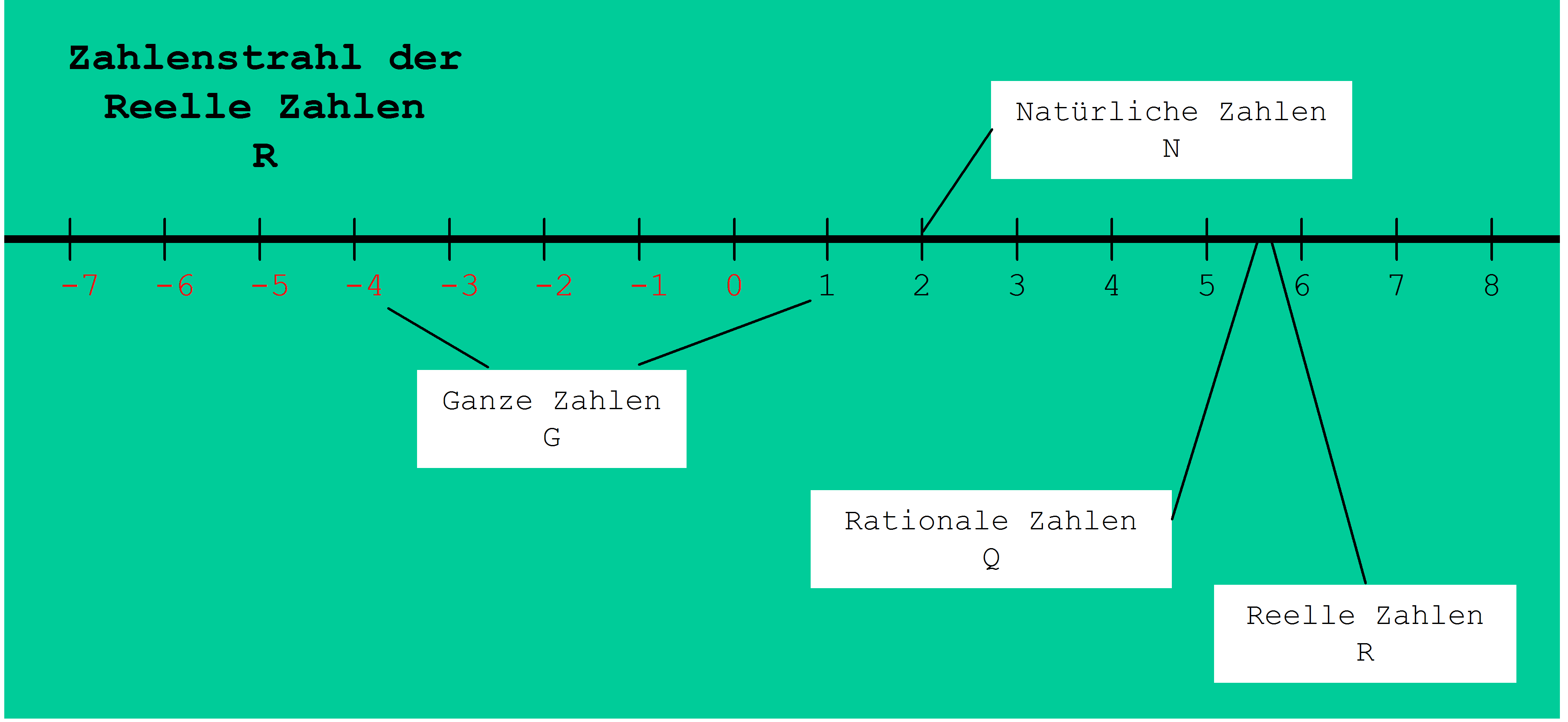
Werden die Zahlen ihrem Wert entsprechend auf einer Geraden angeordnet, spricht man von einer Zahlengeraden (Abbildung 15). Auf dieser Geraden ist die Gesamtheit der Reellen Zahlen als Kontinuum angeordnet. Da die Rationalen, die Ganzen und die Natürlichen Zahlen echte Teilmengen
\( ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ \)
der Reellen Zahlen sind, finden sich diese Mengen ebenfalls auf dem Zahlenstrahl wieder. Weil sie aber abzählbar sind, sind sie punktuell auf dem Zahlenstrahl zu finden. Überabzählbare Zahlen, wie die Reellen Zahlen, treten hingegen als Kontinuum auf.
Sind nun zwei Zahlen a und b, (a < b) gegeben, stecken sie die Grenzen eines Zahlenbereiches, eines Intervalls ab. Das Intervall heißt
-
geschlossen, wenn a und b zum Intervall gehören -
Schreibweise: [a,b], -
offen, wenn a und b außerhalb des Intervalls liegen -
Schreibweise: (a,b), -
halboffen, wenn eine der beiden Grenzen innerhalb, die andere Grenze außerhalb des Intervalls liegen -
Schreibweise: (a,b] bzw. [a,b).
Jedes Intervall schließt eine Teilmenge der Reellen Zahlen ein. Das nach oben und unten offene Intervall (-∞, ∞) ist die Grundmenge der Reellen Zahlen selbst.
