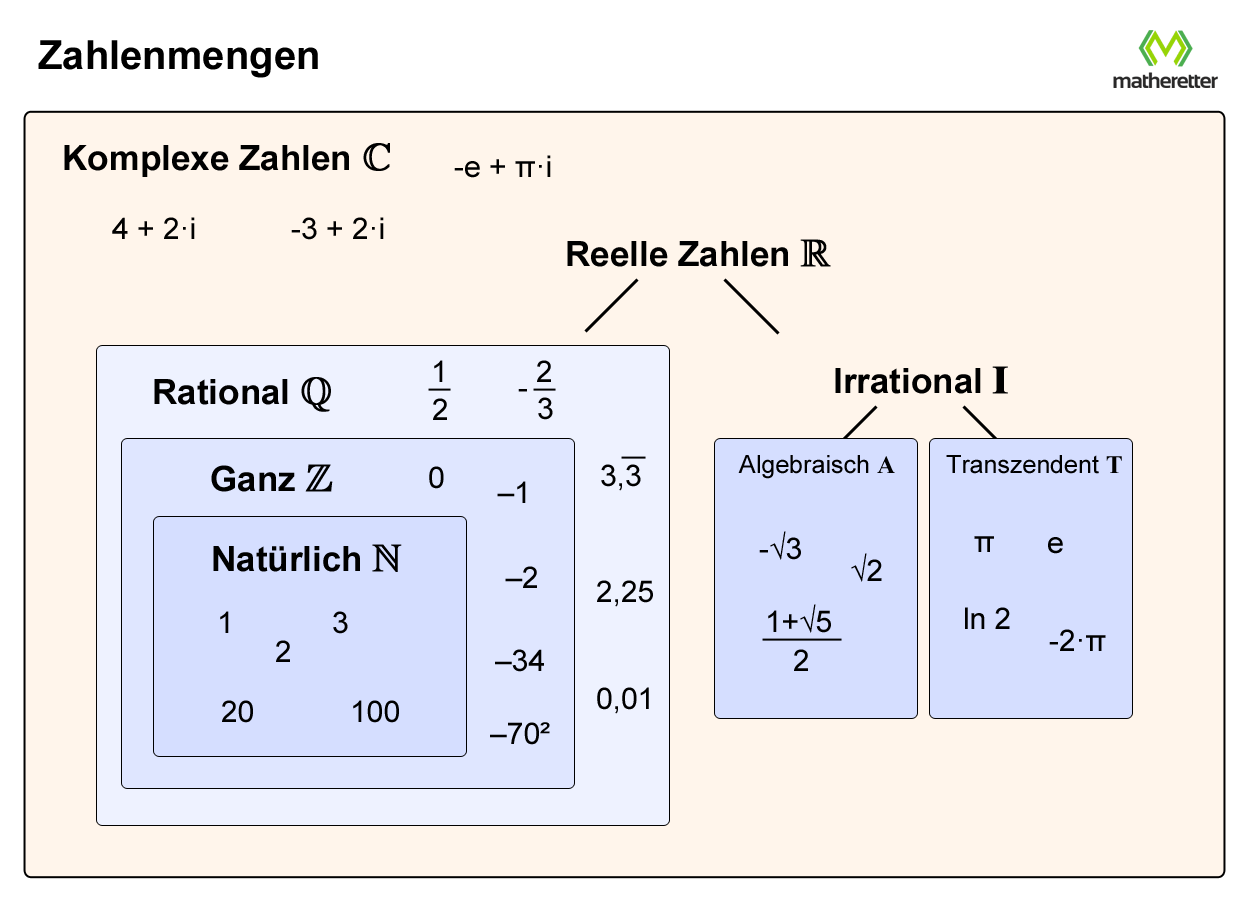
Definition der reellen Zahlen
Die reellen Zahlen ergeben sich aus der Menge der rationalen Zahlen ℚ und der irrationalen Zahlen I.
Für diese Zahlenmenge verwenden wir das Zeichen ℝ.
\( \mathbb{R} = \{ \ldots; -2,5; -2; -1; -0,\overline{3}; 0; \allowbreak \frac{1}{2}; 1; 2; e; 3; \pi; \ldots \} \)
\( \mathbb{R} = \mathbb{Q} \cup \mathbb{I} \)
Grafik zur Darstellung der Zahlenmengen
Die folgende Grafik stellt die Zahlenmengen dar. Wir erkennen, welche Zahlenmengen die reellen Zahlen umschließen.
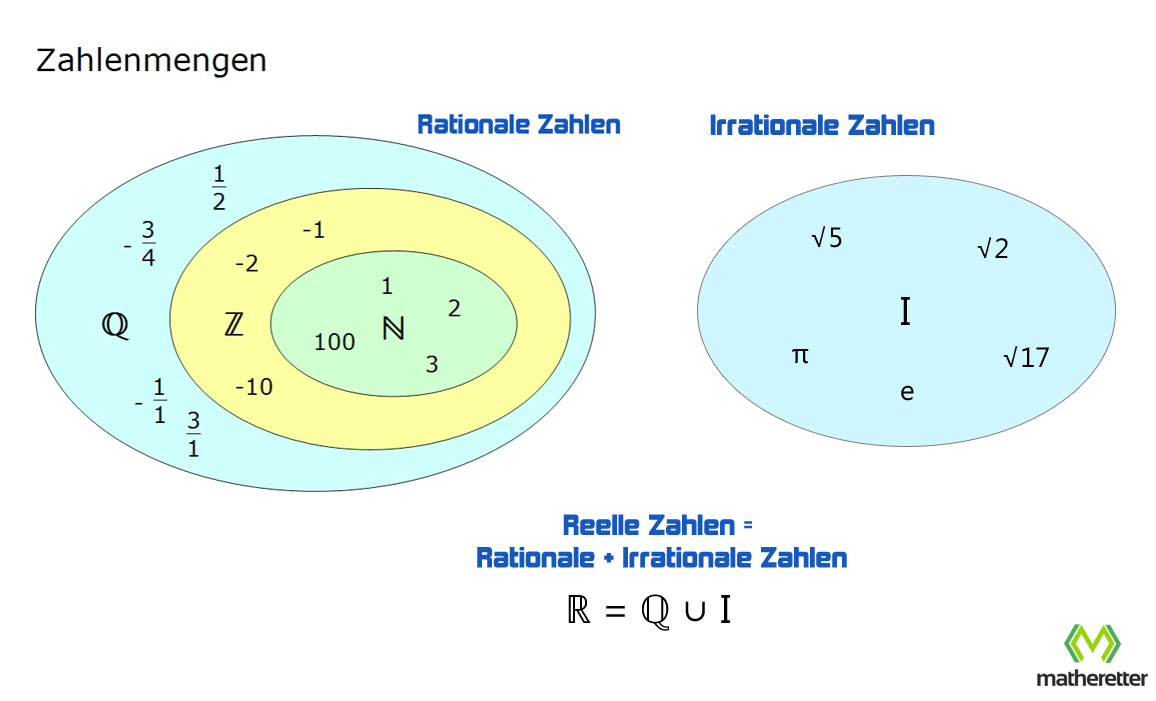
Teilmengen der Reellen Zahlen
Es kann vorkommen, dass wir nur die positiven reellen Zahlen angeben sollen oder nur die negativen. Im Folgenden die korrekten Schreibweisen hierfür:
| Teilmenge | Zeichen | Definition | Latex-Code |
| Positive reelle Zahlen | \( \mathbb{R}^{+} \) | \( x | x \in \mathbb{R}, x > 0 \) | \mathbb{R}^{+} |
| Positive reelle Zahlen inklusive Null | \( \mathbb{R}_0^{+} \) | \( x | x \in \mathbb{R}, x \geq 0 \) | \mathbb{R}_0^{+} |
| Negative reelle Zahlen | \( \mathbb{R}^{-} \) | \( x | x \in \mathbb{R}, x < 0 \) | \mathbb{R}^{-} |
| Negative reelle Zahlen inklusive Null | \( \mathbb{R}_0^{-} \) | \( x | x \in \mathbb{R}, x \leq 0 \) | \mathbb{R}_0^{-} |
| Reelle Zahlen ohne Null | \( \mathbb{R}^{*} \) | \( x | x \in \mathbb{R}, x \neq 0 \) | \mathbb{R}^{*} |
Die folgende Abbildung stellt die reellen Zahlen dar sowie die komplexen Zahlen, die wir uns im nächsten Artikel anschauen werden.