Die komplexen Zahlen werden notwendig, wenn man Lösungen finden möchte für Gleichungen wie x2 = -9. Haben wir nur die reellen Zahlen zur Verfügung, so würden wir schreiben x = nicht definiert, da es keine reelle Zahl gibt, die quadriert -9 ergibt.
Hier helfen uns die komplexen Zahlen weiter:
Die komplexen Zahlen sind eine Erweiterung der reellen Zahlen. Es wird eine „imaginäre Einheit“ mit i2 = -1 eingeführt. Dadurch lassen sich u. a. auch Wurzeln aus negativen Werten ziehen.
Die Zahlenmenge der komplexen Zahlen hat das Zeichen ℂ.
Mit Hilfe der imaginären Einheit i2 = -1 können Lösungsmengen bestimmt werden, die im reellen Zahlenbereich nicht existieren.
Lösen wir eine entsprechende quadratische Gleichung:
\( x^2 = -9 \\ x^2 = -1 · 9 \quad | -1 = i^2 \\ x^2 = i^2 · 9 \\ x_1 = +\sqrt{i^2} · \sqrt{9} = +i · 3 \\ x_2 = -\sqrt{i^2} · \sqrt{9} = -i · 3 \)
Die Lösungsmenge lautet: L = { +i · 3; -i · 3 }
Jede komplexe Zahl setzt sich zusammen aus einer imaginären Zahl und einer reellen Zahl.
Wir notieren:
Komplexe Zahl = Realteil + Imaginärteil
z = a + b·i
Wobei a, b ∈ ℝ.
Damit gilt außerdem die Mengenzuordnung:
\( \mathbb N \subset \mathbb Z \subset \mathbb R \subset \mathbb C \)
bzw.
\( \mathbb N \subset \mathbb Z \subset (\mathbb{Q} \cup \mathbb{I}) \subset \mathbb C \)
Wir können die Menge der komplexen Zahlen so festhalten:
\( \mathbb{C} = \{ \ldots, i, 1 + 3·i, 4 - 2·i, \ldots \} \)
Allgemein definiert man die komplexen Zahlen mit:
\( \mathbb{C}=\{z = a + b·i | a,b \in \mathbb{R}, i = \sqrt{-1}\} \)
Komplexe Zahlen im Koordinatensystem
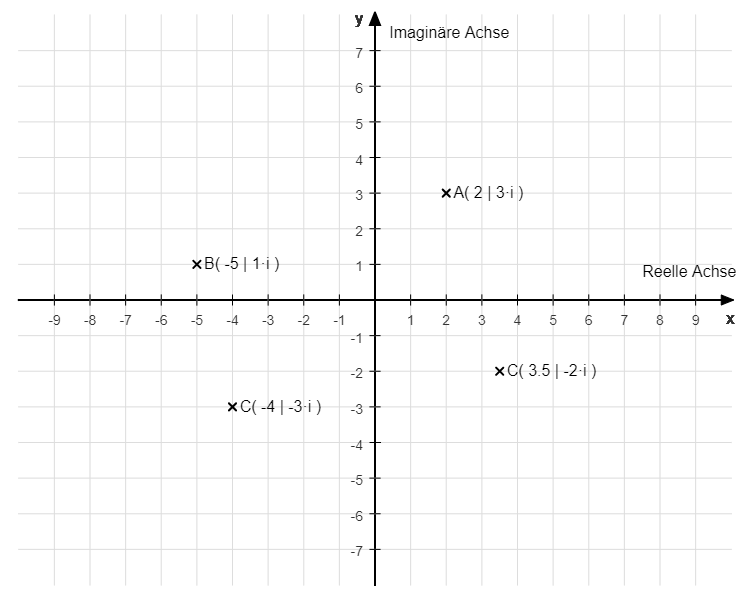
Nachstehend werden die komplexen Zahlen im kartesischen Koordinatensystem dargestellt.
In der obigen Abbildung sehen wir verschiedene Beispiele von komplexen Zahlen.
Punkt A: Der Realteil ist 2 und der Imaginärteil ist 3. Dadurch ergibt sich die komplexe Koordinate (2|3·i). 2 befindet sich auf der reellen Achse (horizontal) und 3 befindet sich auf der imaginären Achse (vertikal).
Punkt B: Der Realteil ist -5 und der Imaginärteil ist 1. Dadurch ergibt sich die komplexe Koordinate (-5|1·i). -5 befindet sich auf der reellen Achse und 1 befindet sich auf der imaginären Achse.
Punkt C: Der Realteil ist -4 und der Imaginärteil ist -3. Dadurch ergibt sich die komplexe Koordinate (-4|-3·i). -4 befindet sich auf der reellen Achse und -3 befindet sich auf der imaginären Achse.
Punkt D: Der Realteil ist 3,5 und der Imaginärteil ist -2. Dadurch ergibt sich die komplexe Koordinate (3,5|-2·i). 3,5 befindet sich auf der reellen Achse und -2 befindet sich auf der imaginären Achse.