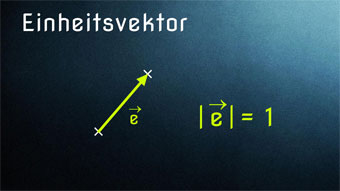
Lektion VEK06: Einheitsvektor
Nach der Skalarmultiplikation lernen wir nun den Einheitsvektor kennen. Jeder Vektor mit der Länge 1 wird als Einheitsvektor bezeichnet.
Weitere Videos für Kunden:
-
VEK06-1 EinheitsvektorWas ist der Einheitsvektor und wie berechnen wir seine Komponenten. Was sind Basisvektoren.
-
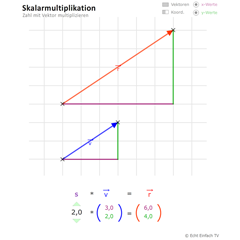 SkalarmultiplikationHier könnt ihr eine Zahl (sog. Skalar) mit einem Vektor multiplizieren. Der Vektor streckt oder staucht sich je nach Wert des Skalars. Bei negativen Werten ändert der Vektor seine Richtung.
SkalarmultiplikationHier könnt ihr eine Zahl (sog. Skalar) mit einem Vektor multiplizieren. Der Vektor streckt oder staucht sich je nach Wert des Skalars. Bei negativen Werten ändert der Vektor seine Richtung. -
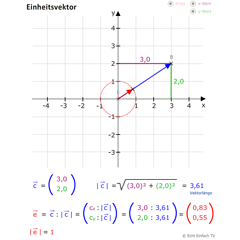 EinheitsvektorErstelle einen beliebigen Vektor und der Einheitsvektor wird aus den Komponenten berechnet.
EinheitsvektorErstelle einen beliebigen Vektor und der Einheitsvektor wird aus den Komponenten berechnet.
Hier findest du 1 Arbeitsblatt, mit dem du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Artikel im Wiki:
Häufige Fragen:
- Richtige Notation des Einheitsvektors?
- Einheitsvektor bilden für Vektor b mit: 3e_x - 4e_y + 8e_z
- Einheitsvektor in Richtung von a=(9|-12)?
- Einheitsvektor e ist ein Vektor mit …?
Finde weitere Fragen und Antworten in der Mathelounge.