Ableitung
Die Ableitungsfunktion über die h-Methode zu bestimmen ist weiterhin aufwändig. Deshalb bestimmt man die Ableitung (Kurzform für Ableitungsfunktion) mittels der h-Methode nur wenige Male - sie dient dem Verständis -, und merkt sich ansonsten die wichtigsten Ableitungen. Um das Auswendiglernen zu erleichtern, gibt es eine ganze Reihe von Hilfestellungen bzw. als bekannt vorausgesetzte Ableitungen; so merkt man sich diese überschaubare Anzahl und bildet die Ableitung der gewünschten Funktion.
Die wichtigsten Ableitungen in tabellarischer Form aufgezeigt.
| Funktion f(x) | Ableitung f'(x) | |
| Potenzfunktion | xn | n·xn-1 |
| Konstante | k | 0 |
| e-Funktion | ex | ex |
| Logarithmus | ln(x) | \( \frac{1}{x} \) |
| Sinus | sin(x) | cos(x) |
| Kosinus | cos(x) | -sin(x) |
| Tangens | tan(x) | \( \frac{1}{cos^2(x)} \) |
All diese Ableitungen könnte man mit der h-Methode herleiten, doch werden sie meist als bekannt vorausgesetzt und eine Herleitung ist nicht nötig. Schauen wir uns noch ein paar Beispiele zur Potenzfunktion an, die wohl eine der wichtigsten Ableitungen überhaupt ist.
Beispiel
Es seien gegeben: f(x) = x, g(x) = x² und h(x) = x³. Es sollen die Ableitungen bestimmt werden, in dem man die Potenzfunktion annimmt.
f(x) = x = x1, somit n = 1
f'(x) = 1·x1-1 = x0 = 1
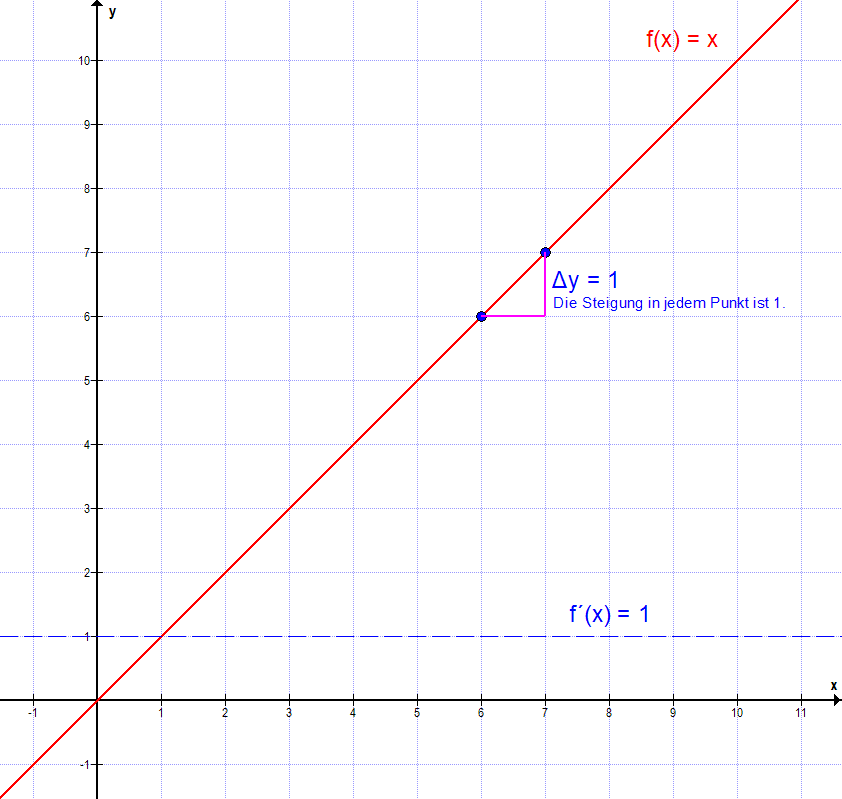
Dass die Ableitung von f(x) korrekt ist, können wir direkt ablesen, denn die Steigung ist stets 1, und somit auch die Ableitung f'(x) = 1. g(x) hatten wir bereits mit der h-Methode verifiziert. So könnten wir auch die Ableitung von h(x) bestätigen und dann die Potenzregel für sich.
g(x) = x², somit n = 2
g'(X) = 2·x2-1 = 2·x
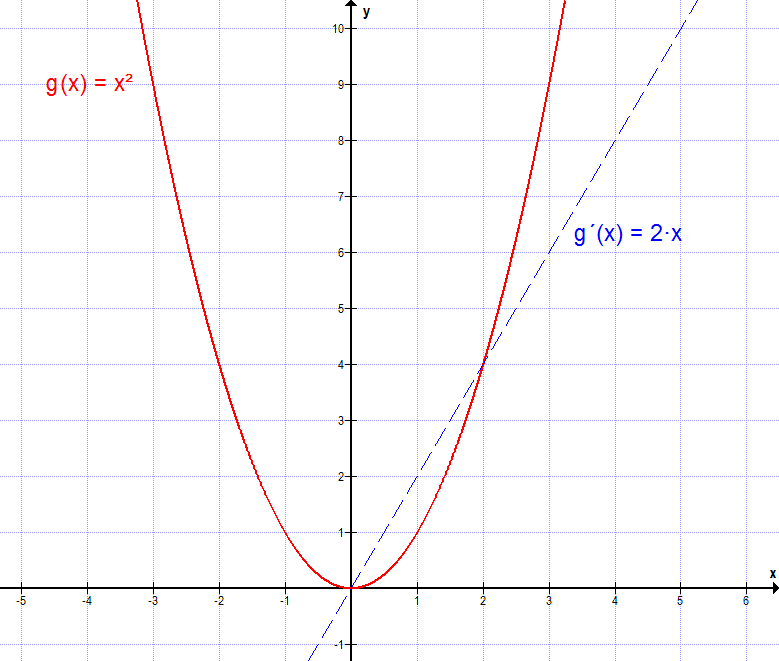
h(x) = x³, somit n = 3
h'(x) = 3·x3-1 = 3·x²
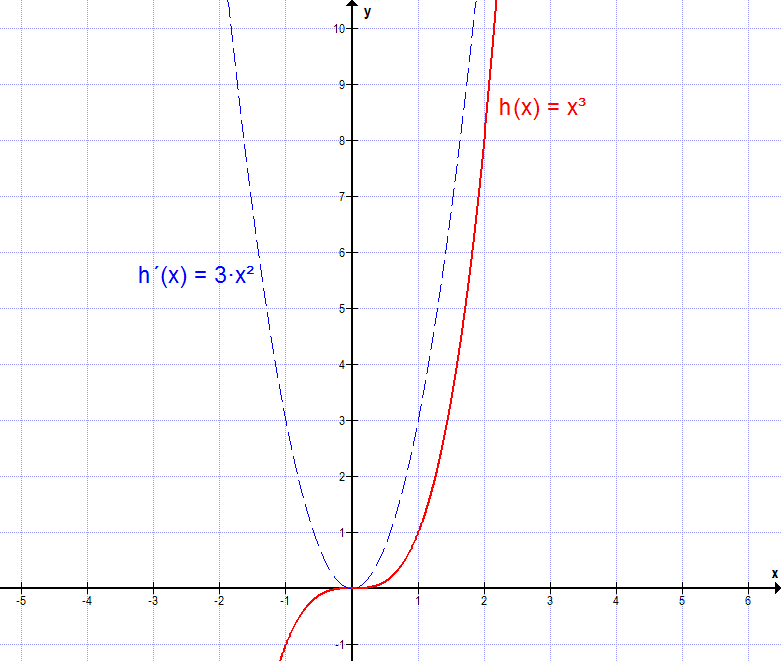
Anmerkung: Die Ableitung einer Konstanten, ist immer 0. Es gibt keine positive oder negative Steigung bei einem waagerechten linearen Graphen. So haben wir k(x) = 3 und k'(x) = 0.