Was ist der Differentialquotient?
Greifen wir den Gedanken vom Ende des letzten Kapitels Differenzenquotient auf:
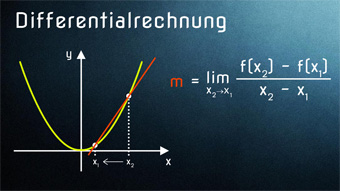
Wir hatten angemerkt, dass wir die Steigung einer Funktion umso genauer bestimmen können, je näher sich die Punkte P1 und P2 kommen. Der Idealfall träfe ein, sobald sich die beiden Punkte berühren. Wenn sich die beiden Punkte aber berühren (also praktisch identisch sind) haben wir es nicht mehr mit einer Sekante zu tun, sondern mit einer Tangente.
Hierin besteht auch der Unterschied zwischen dem Differenzenquotienten und dem Differentialquotienten. Um dem Differentialquotienten Ausdruck verleihen zu können, nutzen wir den Grenzwert. Der modifizierte Ausdruck hat die Gestalt:
\( m = \lim_{x_2 \to x_1} \frac{f(x_2) - f(x_1)}{x_2 - x_1} = \frac{\Delta y}{\Delta x} \)
Der Grenzwert beschreibt also die Annäherung des einen x-Wertes an den anderen x-Wert und damit die Annäherung der beiden Punkte.
Mit Hilfe des Differentialquotienten kann man schon sehr genaue Aussagen über das Steigungsverhalten einer Kurve in einem Punkt treffen. Doch ist das Verfahren zur Bestimmung des Differentialquotienten sehr aufwändig.
Beispiel
Wenn wir die Steigung der Funktion f(x) = x² an der Stelle x1 = 3 bestimmen wollen, so gehen wir wie folgt vor:
x1 = 3
f(x1) = (x1)² = y
f(x1) = 3² = 9
x2 lassen wir als solches stehen, dies soll sich ja an x1 annähern (das setzen wir in den Limes).
f(x2) = (x2)²
In die Formel:
$$ m = \lim_{x_2 \to x_1} \frac{f(x_2) - f(x_1)}{x_2 - x_1} \\[10pt] m = \lim_{x_2 \to 3} \frac{(x_2)^2 - 9}{x_2 - 3} \\[10pt] m = \lim_{x_2 \to 3} \frac{(x_2 - 3)(x_2+3)}{x_2 - 3} \\[10pt] m = \lim_{x_2 \to 3} x_2+3 = 3 + 3 = 6 $$
Um nicht den Differentialquotienten erneut bestimmen zu müssen, um einen weiteren Punkt auf das Steigungsverhalten zu analysieren, wäre es hilfreich eine Ableitungsfunktion zu kennen, bei der man einen beliebigen x-Wert einsetzt und die zugehörige Steigung erhält.
Da es dem Verständnis zuträglich ist, die Bestimmung einer Ableitungsfunktion einmal gesehen zu haben, befassen wir uns mit der h-Methode und schauen uns das genauer an.