Das grafische Ableiten bzw. „zeichnerisches Differenzieren“ wird meist zur Einführung in die Differentialrechnung verwendet. Als Vorwissen benötigen wir nur die Steigung bei den linearen Funktionen, dann fällt das Verstehen relativ leicht.
Einführung der „Ableitung“
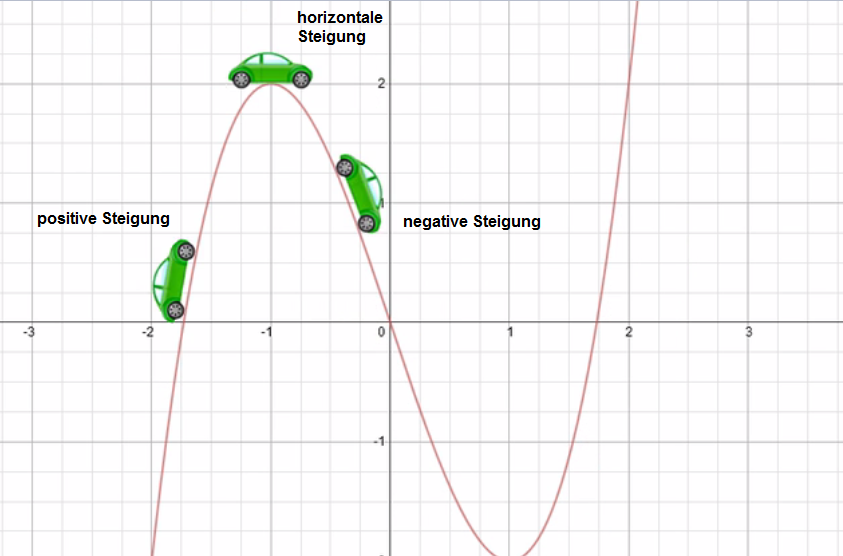
Haben wir einen Graphen vorliegen, so möchte man vielleicht wissen, an welchen Bereichen (oder auch nur Stellen) der Graph eine positive Steigung oder eine negative Steigung besitzt - oder ob er horizontal verläuft.
Wann welche Steigung vorliegt, kann man sich sehr gut mit einem Auto vorstellen, das auf dem Graphen entlang fährt. Sobald dieses nach „oben“ fährt, haben wir eine positive Steigung vorliegen. Fährt es nach „unten“, liegt eine negative Steigung vor und fährt es auf der x-Achse bzw. parallel dazu, so verläuft die Steigung horizontal.
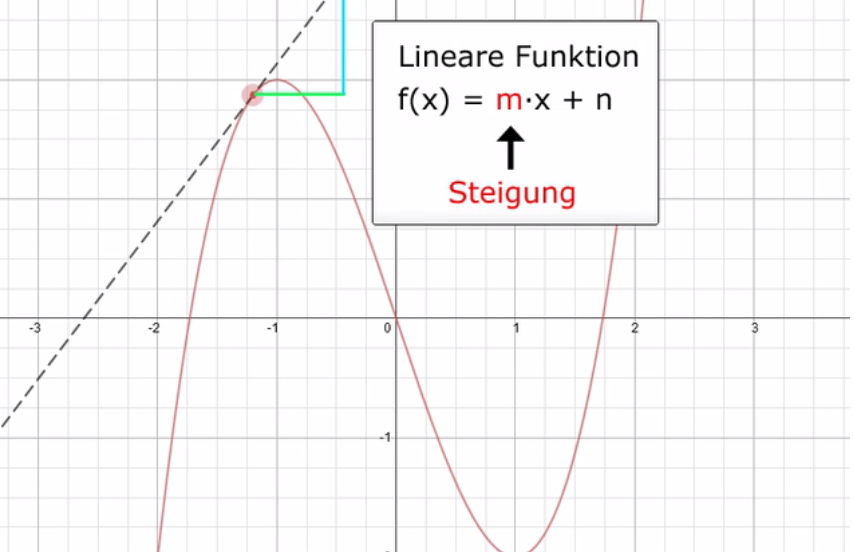
Um nicht jedes Mal ein Auto zeichnen zu müssen, um zu überprüfen, welche Art von Steigung vorliegt, sondern der Steigung sogar einen Wert zuordnen zu können, kann man mit Tangenten arbeiten und deren Steigungen bestimmen.
Dazu erinnern wir uns, dass eine Tangente eine gerade Linie ist, die an einem Graphen anliegt, ihn also nur berührt (im Berührpunkt). Von dieser Tangente aus kann man dann ein Steigungsdreieck anlegen und die Steigung im Berührpunkt bestimmen, was die Steigung des Graphen an dieser Stelle bezeichnet.
Wenn man sich nicht nur eine Stelle anschauen will, sondern Informationen bezüglich der Steigung an allen Stellen haben möchte, so nutzt man die „Ableitung“ der Funktion. Die zugehörige Ableitungsfunktion erlaubt das Ablesen der Steigung in jedem beliebigen Punkt.
Hier wollen wir uns in erster Linie mit der graphischen Bestimmung der Ableitungsfunktion befassen. Um die Funktion aufzustellen, wird obiges Verfahren mit den Tangenten mehrfach wiederholt.
An den Stellen, an denen die Steigung des Graphen bestimmt wird, werden die Steigungen als y-Werte abgetragen. Damit ergeben sich Punkte, die sinnvoll zu einem neuen Graphen verbunden werden können.
Schauen wir uns das im Folgenden an:
Zuerst das Ablesen der Steigung an einer beliebigen Stelle (hier x = -1).
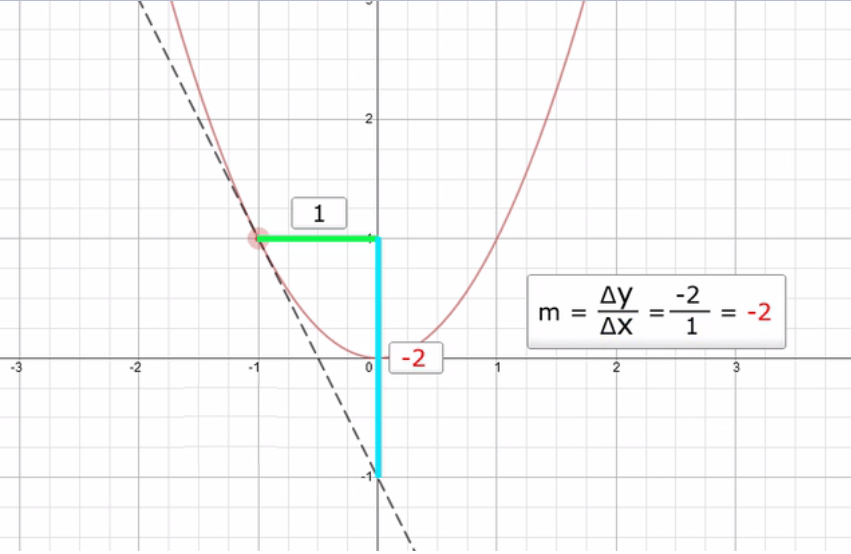
Der Wert der Steigung (hier m = -2) wird als y-Wert an der untersuchten Stelle x = -1 eingesetzt, also bei y = -2. Der Punkt wird demnach eingetragen mit P`(-1|-2).
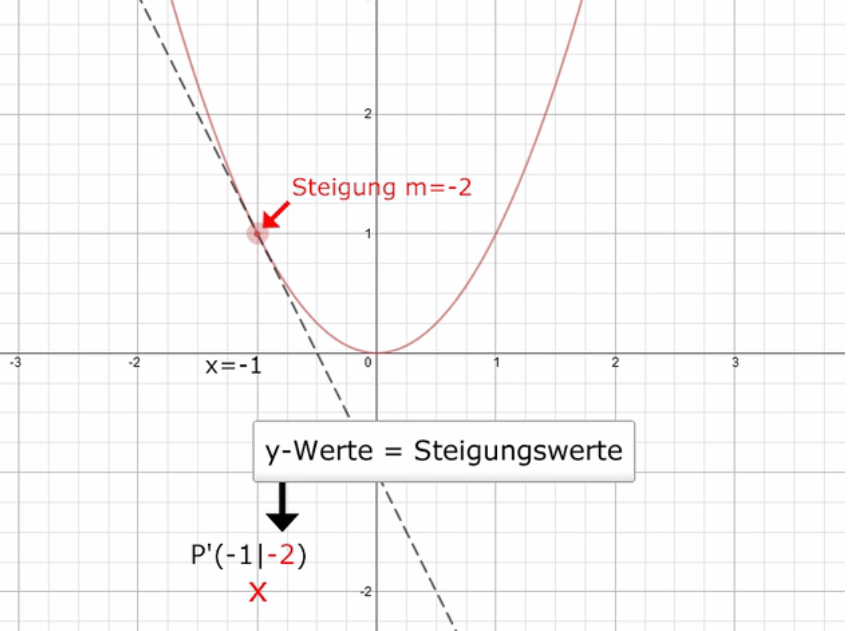
Man nimmt sich weitere Stellen vor und macht das so lange, bis man sich ein Bild der Ableitungsfunktion bilden kann.
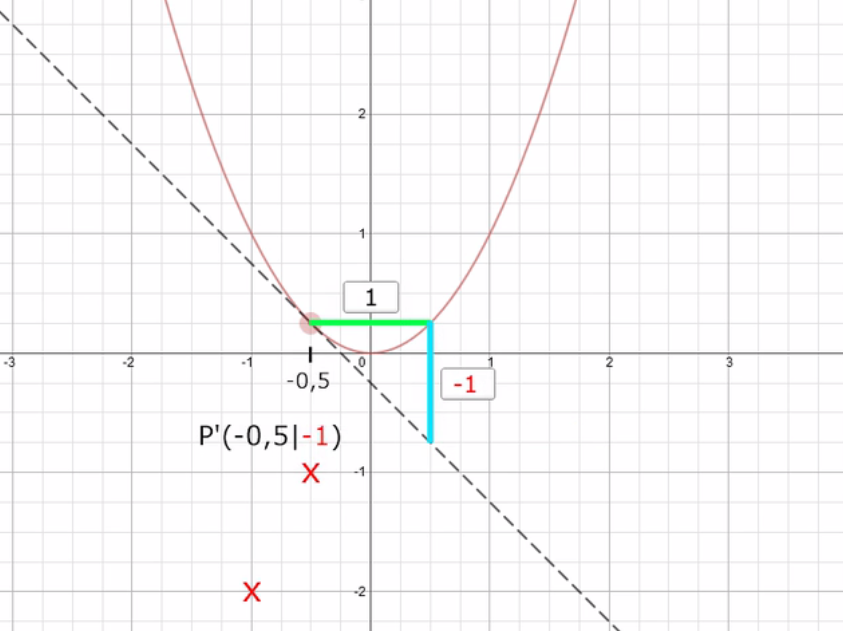
Im folgenden Bild haben wir mehrere Stellen untersucht und die neuen Punkte (der Ableitungsfunktion) eingetragen. Wir erkennen, dass es sich um eine Gerade handeln muss.

Liest man die Steigung der Geraden ab, so stellt sich heraus, dass m = 2 sein muss. Die Gerade kann nun angegeben werden als f‘(x) = 2·x und ist die Ableitungsfunktion von f(x) = x².
Der Strich am f macht dabei deutlich, dass es sich um die Ableitung handelt. Wie wir später kennen lernen, wird beispielsweise die zweite Ableitung mit f‘‘ bezeichnet.
Vorgehen beim grafischen Ableiten
Das allgemeine Vorgehen ist in folgende Schritte gegliedert:
- Lege eine Tangente an einen Punkt, damit du die Steigung in diesem Punkt bestimmen kannst.
- Die Tangentensteigung wird zum y-Wert (zur gleichen Stelle x).
- Die Zuordnung von x- und y-Werten ergibt die Punkte der Ableitungsfunktion.
Die Schritte 1. und 2. werden mehrfach ausgeführt, bis sich ein Bild der Ableitungsfunktion ergibt.
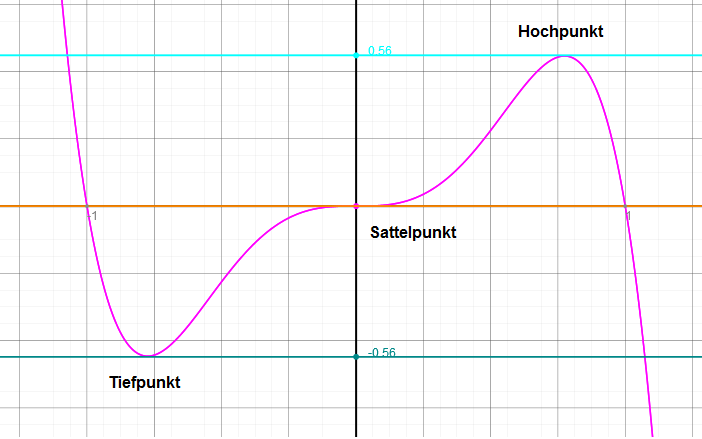
Spezialfälle: Hochpunkt, Tiefpunkt, Wendepunkt
Für den Fall, dass eine Tangente parallel zur x-Achse verläuft, die Steigung also mit m = 0 beziffert werden kann, liegt ein Spezialfall vor, dem man sogar einen besonderen Namen gibt.
Die Punkte, die diese Steigung aufweisen, werden als „mögliche Extrempunkte“ bezeichnet.
Spricht man nur von der Stelle, spricht man vom „Extremum“ (Plural „Extrema“).
Dabei unterscheidet man drei verschiedene Fälle, die sich aus dem Graphen ergeben:
Es gibt den Hochpunkt und den Tiefpunkt, was nichts anderes bedeutet, dass in der näheren Umgebung kein y-Wert größer bzw. kleiner ist. Hierbei handelt es sich dann in der Tat um Extrema bzw. Extrempunkte.
Weiterhin gibt es den sogenannten Sattelpunkt, ein Spezialfall des Wendepunktes. Beim Sattelpunkt haben wir auf einer Seite einen größeren y-Wert und auf der anderen Seite einen kleineren y-Wert, dies wäre also kein Extrempunkt.
Im Schaubild: