In der Schule weniger geläufig, aber weiterhin wichtig: Die Formel für die Symmetrie zu einer beliebigen Senkrechten (Achsensymmetrie) lautet:
f(a+x) = f(a-x)
Mit dem a berücksichtigen wir die Verschiebung der Symmetrieachse.
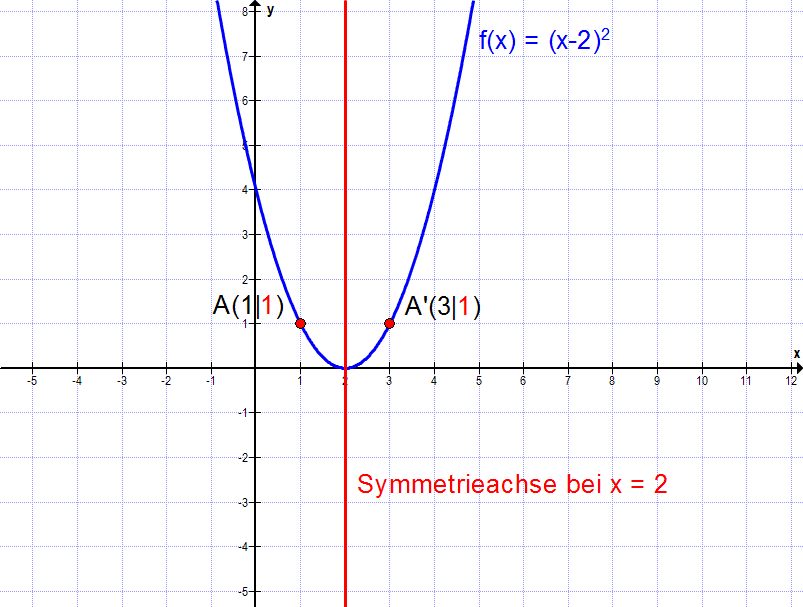
Für die Verschiebung der Parabel um 2 nach rechts erhalten wir die Funktionsgleichung f(x) = (x-2)2. Der y-Wert für x = 1 ist f(1) = (1-2)2 = 1 = y.
Mit der obigen Formel können wir den Punkt finden, der ebenfalls den y-Wert 1 besitzt.
Es gilt f(a+x) = f(a-x), wobei a = 2. Da wir uns bereits x = 1 angeschaut haben, wird nun x = 1 eingesetzt:
f(2+1) = f(2-1) → f(3) = f(1)
An der Stelle x = 3 finden wir also ebenfalls den y-Wert y = 1.
f(a+x) = f(a-x)
f(2+1) = f(2-1)
f(3) = f(1)
1 = 1
Das sieht man auch am Graphen: