Die Formel für die Symmetrie zu einem beliebigen Punkt (Punktsymmetrie) lautet:
f(a+x)-b = -f(a-x)+b
Hier berücksichtigen wir mit b die Verschiebung des Graphen nach oben oder unten.
Das Symmetriezentrum S(a|b) ist der Punkt, an dem sich die Symmetrie orientiert. Für die Symmetrie zum Koordinatenursprung ist es Z(0|0).
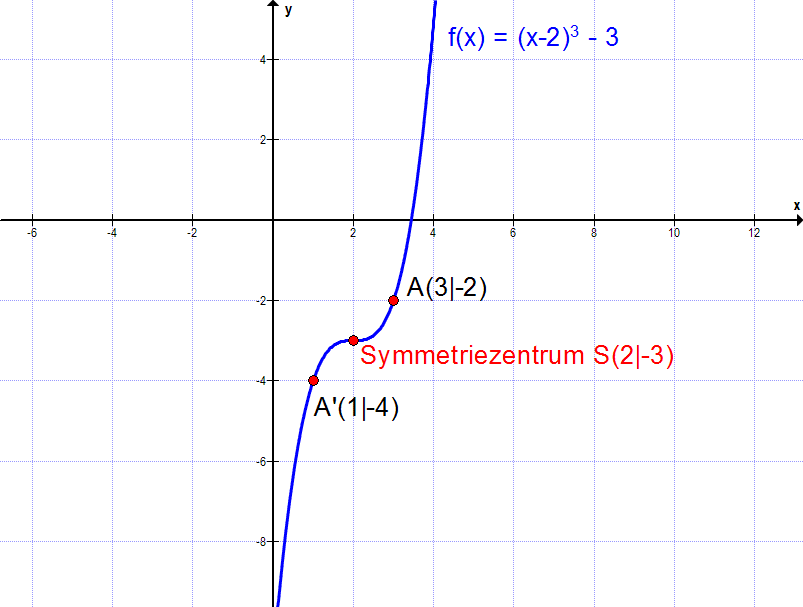
Um ein Beispiel anzuführen nehmen wir die kubische Funktion f(x) = (x - 2)3 - 3 (Graph siehe unten).
Der Symmetriepunkt liegt somit bei S(2|-3). Der y-Wert zu x = 1 ist f(1) = (1 - 2)3 - 3 = -4. Den y-Wert, welcher bei x = 3 zu erwarten ist, also 1 Einheit rechts vom Symmetriezentrum, errechnen wir mittels obiger Formel. Dabei ist x = 1, a = 2 und b = -3.
f(a+x) - b = -f(a-x) + b
f(2+1) - (-3) = -f(2-1) + (-3)
f(3) + 3 = -f(1) - 3
f(3) + 3 = -(-4) - 3
f(3) + 3 = 1 | -3
f(3) = -2
Wir sehen bereits in der zweiten Zeile, dass die gleiche Entfernung zum Symmetriezentrum vorliegt (1 nach links, 1 nach rechts). Für x = 3 erhalten wir f(3) = (3-2)3 - 3 = -2. Das sieht man auch gut am Graphen: