Die Formel für die Symmetrie zum Koordinatenursprung lautet (Punktsymmetrie):
f(x) = -f(-x)
Jetzt werden nicht nur die x-Werte umgekehrt, sondern auch die dazugehörigen y-Werte.
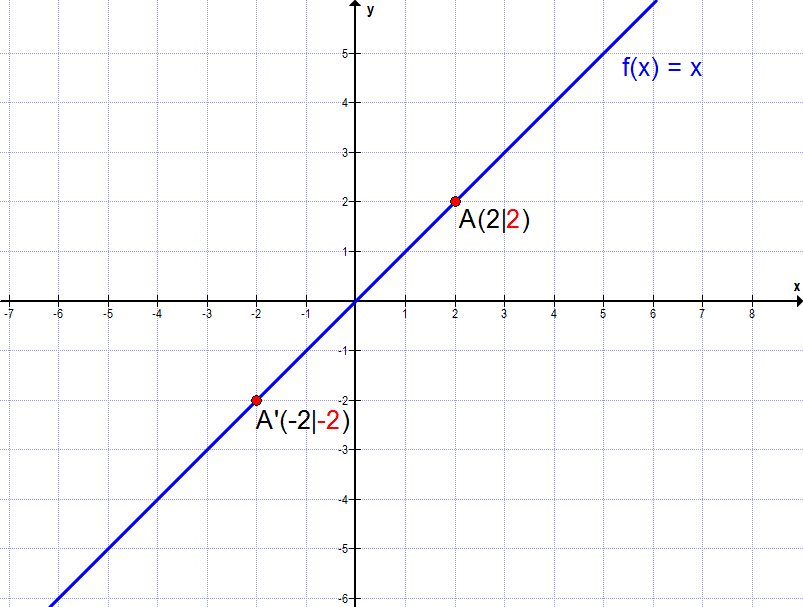
Ein Beispiel hierfür wäre die Gerade f(x) = x. Wählen wir beispielhaft den x-Wert x = 2, so erhalten wir den y-Wert f(2) = 2 = y. Nehmen wir nun den x-Wert mit dem entgegengesetzten Vorzeichen x = -2 wird der y-Wert -2 erwartet (also ebenfalls mit umgekehrtem Vorzeichen). Dem ist auch so: f(-2) = -2.
f(x) = -f(-x)
f(2) = -f(-2)
4 = -(-4)
4 = 4
Auch gut am Graphen zu erkennen: