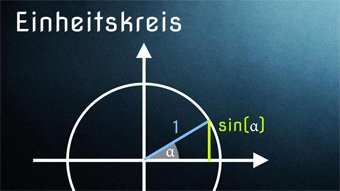
Wir wollen alle Sinus- und Kosinuswerte am Einheitskreis ablesen. Im Folgenden erläutern wir, wie das geht.
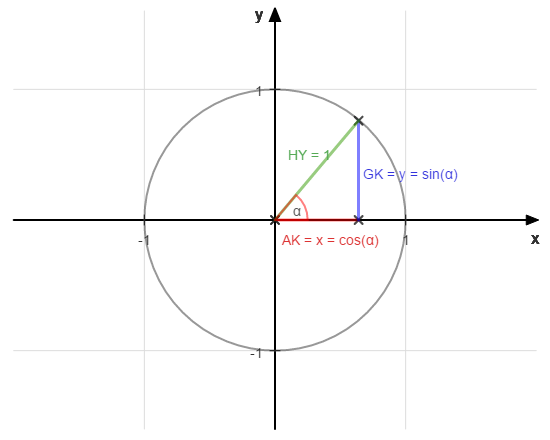
Wir sehen, dass beim Einheitskreis die Gegenkathete (siehe Wert auf der y-Achse) den Sinuswert angibt und die Ankathete (siehe Wert auf der x-Achse) den Kosinuswert.
Wir merken uns:
sin(α) = Höhe = y
cos(α) = Breite = x
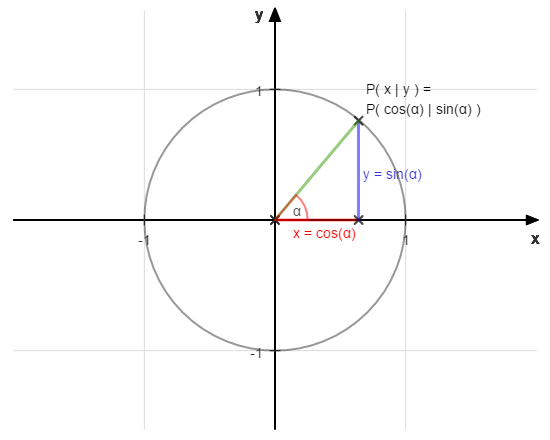
Genausogut können wir sagen, der Punkt auf der Kreislinie mit P(x|y) trägt die Sinus- und Kosinuswerte in seinen Koordinaten:
P( x | y ) = P( cos(α) | sin(α) )
Wir merken uns:
Im Einheitskreis entspricht die Gegenkathete dem Sinuswert und die Ankathete dem Kosinuswert, wobei auf die Vorzeichen zu achten ist. Ebenfalls gilt: Die Koordinaten des Punktes P auf der Kreislinie des Einheitskreises geben Kosinuswert (x) und Sinuswert (y) an.
Winkel mit Sinus und Kosinus positiv bzw. negativ
Je nach gewähltem Winkel erhalten wir auch negative Werte für Sinus, Kosinus und Tangens. Hier ein Übersicht mit den vier Quadranten:
|
II. Quadrant
sin + cos – tan – |
I. Quadrant
sin + cos + tan + |
|
III. Quadrant
sin – cos – tan + |
IV. Quadrant
sin – cos + tan – |
Wir sehen: Sinus ist im I. und II. Quadranten positiv ("oben"), Kosinus ist im I. und IV. Quadranten positiv ("rechts") und Tangens ist im I. und III. Quadranten positiv. Negative Werte erhalten wir für Sinus im III. und IV. Quadranten ("unten"), für Kosinus im II. und III. Quadranten ("links") und für Tangens im II. und IV. Quadranten.