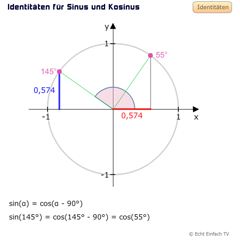
Diese Identität muss man nicht einzeichnen, denn sie besagt, dass wenn wir einmal im Kreis herumgehen, sich unser Punkt P wieder an der gleichen Position befindet und damit Sinus- und Kosinuswerte für beide Winkel dieselben sind.
Das Programm "Einheitskreis: Identitäten für Sinus und Kosinus" zeigt die vorgenannten und weitere Identitäten auf. Dort sehen wir animiert, wie sich die Identitäten verhalten.